analiza matematyczna zbiory
grzesiuu: Dobry wieczór!
Mam do rozwiązania taki przykład:
Narysuj zbiory:
a) {(x,y) ∈ R2 : |x| + |y| > 1, x2 + y2 ≤ 1}, jednak nie rozumiem co oznacza zapis R2,
rzeczywiste nieujemne?
Z góry dzięki.
1 paź 21:35
sushi_gg6397228:
x ∊ R i y ∊ R
1 paź 21:36
grzesiuu: A w jakim celu jest wstawiony ten kwadrat przy R?
1 paź 21:42
Eta:
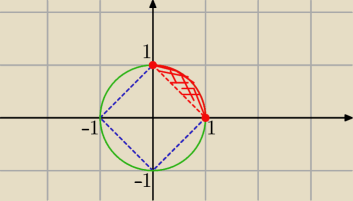
1 paź 21:44
:): R2 znaczy RxR czyli, że elementami R2 są pary liczb (x,y) :x∊R oraz y∊R
np 1∊R , ale (−1,3)∊R2
1 paź 21:47
grzesiuu: Ogromne dzięki!

1 paź 21:49
grzesiuu: Eta, a czy pozostałe 3 cześći pomiędzy rombem a kołem nie powinny być również zamalowane?
1 paź 21:56
Eta:
Napisałeś założenie dla liczb rzeczywistych nieujemnych
zatem tylko te punkty,które zaznaczyłam spełniają ten warunek
1 paź 22:03
:): Nie no..mysle ze on bardziej pytał czy nieujemnych

1 paź 22:04
:): grzesiuu TAK POWINNY

1 paź 22:05
grzesiuu: Tak, to było tylko pytanie

1 paź 22:06
Eta:
Jak napisał .... tak odpowiedziałam

1 paź 22:06
Eta:
Skoro dla R2 , to i pozostałe też zamalowane
1 paź 22:07
grzesiuu: Proszę o pomoc w jeszcze jednym zadaniu, nie chodzi o całe rozwiązanie, ale o sama metodę jak
należy je zrobić.
Wyznacz szukane zbiory:
f(A)=?, f−1(B)=? dla A=(0,3> i B=<2,4) oraz f(x)=|2x−1|+1.
1 paź 22:18
:): zacznij od narysowania wykresu

zobacz jaka w przedziale (0,3> jest najmniejsza wartość, jaka najmniejszą...
f(A)={f(x);x∊A}
pomyśl i dokończ; )
1 paź 22:20
:): jaka najwieksza**
1 paź 22:21
:): (ta najmniejsza albo najwieksza może nie być osiagana)
1 paź 22:21
grzesiuu: w pierwszym <1,6> ?
1 paź 22:36
:):
f(3)=|2*3−1|=1=6 /najwieksza
| | 1 | |
Najmniejsza wartość jest w |
| |
| | 2 | |
wiec zgadza sie

!
1 paź 22:41
:): | | 1 | |
a takie pytanie do ciebie, ile by było f(A) jeżeli A=(0, |
| >  |
| | 2 | |
1 paź 22:41
grzesiuu: <1,2)
mam nadzieje

1 paź 22:48
:): taaak, zrozumiałes o co mi chodziło tak mi sie zdaje

1 paź 22:54
:): To jak będzie z tym przeciwobrazem

f
−1(B)={x∊R:f(x)∊B}
1 paź 22:55
grzesiuu: Większy problem, mam niestety z B. Proszę też o wskazówkę lub rozwiązanie.
1 paź 22:55
:): B=<2,4)
zaznacz sobie ten zbiór na osi OY i popatrz na definicje

1 paź 22:56
grzesiuu: Chciałbym podstawić 2 i 4 i rozwiązać, ale to chyba jednak nie tak.
1 paź 22:57
:): zacznij od tego zaznaczenia

1 paź 22:57
grzesiuu: <0,2) ?
1 paź 22:58
:):
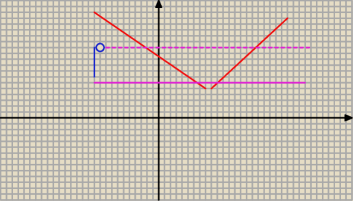
nie za piękny ten rysunek..no ale nich będzie..
to niebieskie to <2,4)
1 paź 23:01
:): f
−1(B)={x∊R:f(x)∊B}
czyli
{x∊R:f(x)∊<2,4)}
czyli
2≤f(x)<4
czyli
2≤|2x−1|+1<4
czyli
1≤|2x−1|<3
|2x−1|=1 => x=0 lub x=1
|2x−1|=3=>x=−1 lub x=4
czyli 1≤|2x−1| oznacza, że x∊(−
∞,0>∪<1,
∞)
|2x−1|<3 iznacza, ze x∊(−1,4)
Zachodzic maja oba warunki wieć
x∊((−
∞,0>∪<1,
∞))∩(−1,4)=...

1 paź 23:06
:): Można wiec też to zrobić "analitycznie", ale jak sie wprawisz..to widać z rysunku
1 paź 23:07
Eta:
"wieć" ... co to oznacza?
1 paź 23:07
:): x=2..nie 4


1 paź 23:08
:): więc

... c ukradło e kreske

i konekwentnie..tam gdzie ejst 4 ma być 2
1 paź 23:09
grzesiuu: Jescze raz dziękuję!
1 paź 23:32
:): spokoo

1 paź 23:33
:): czyli po prostu (−1,0>∪<1,2) jakbyż już spał

1 paź 23:34
grzesiuu: obliczyłem sobie

ale powiem szczerze, że z rysunku to w ogóle tak dla mnie nie wygląda

1 paź 23:38
:): nie no widac....ja sobie przyłożysz poziomo linijke (równolegle do osi OX) i zobaczysz w
których punktach przecina
y=2
i potem
y=4
to zobaczysz, że to oczywiste

1 paź 23:40






 zobacz jaka w przedziale (0,3> jest najmniejsza wartość, jaka najmniejszą...
f(A)={f(x);x∊A}
pomyśl i dokończ; )
zobacz jaka w przedziale (0,3> jest najmniejsza wartość, jaka najmniejszą...
f(A)={f(x);x∊A}
pomyśl i dokończ; )
 !
!



 f−1(B)={x∊R:f(x)∊B}
f−1(B)={x∊R:f(x)∊B}


 nie za piękny ten rysunek..no ale nich będzie..
to niebieskie to <2,4)
nie za piękny ten rysunek..no ale nich będzie..
to niebieskie to <2,4)



 ... c ukradło e kreske
... c ukradło e kreske  i konekwentnie..tam gdzie ejst 4 ma być 2
i konekwentnie..tam gdzie ejst 4 ma być 2


 ale powiem szczerze, że z rysunku to w ogóle tak dla mnie nie wygląda
ale powiem szczerze, że z rysunku to w ogóle tak dla mnie nie wygląda 
