Proporcjonalność odwrotna
Dawid: Wskaż hiperbolę, która ma dokładnie dwa punkty wspólne z okręgiem o środku w punkcie(0,0) i
promieniu 4
Odp. to y=−8/x
Prosiłby o pomoc w rozwiązaniu.
Próbowałem zastosować te dwa wzory: (x−2)2+(y−b)2=r2 oraz y=a/x , ale nie dałem razy
rozwiązać.
1 paź 19:04
5-latek:
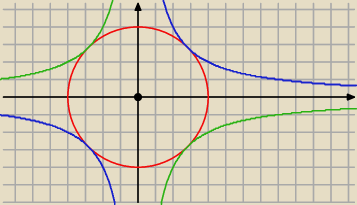
| | −8 | |
faktycznie hiperbola y= |
| (zielona ) ma 2 punkty wspólne z okręgiem |
| | x | |
| | 8 | |
Ale również hiperbola y= |
| (niebieska) tez ma 2 punkty wspólne z okręgiem |
| | x | |
1 paź 19:13
===:
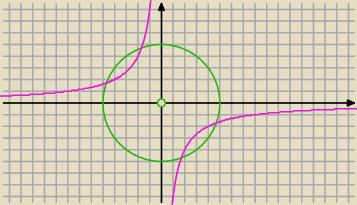
ciekawe ...
1 paź 19:20
5-latek: Na Twoim rysunku jest r=5

1 paź 19:23
===:

... jasne

1 paź 19:24
Dawid: A czy dąłby ktoś radę obliczyć wzór wzór tej hiperboli ?
1 paź 21:08
Janek191:
x
2 + y
2 = 16
więc
x
4 − 16 x
2 + a
2 = 0
x
2 = t > 0
t
2 − 16 t + a
2 = 0
Δ = 256 −4*1*a
2 = 256 − 4 a
2 = 0 ⇒ a
2 = 64 ⇒ a = − 8 lub a = 8
=========================
spr.
t
2 − 16 t + 64 = 0
( t − 8)
2 = 0
x
2 = 8
1 paź 21:27
Janek191:
Ostatni wiersz jest zbędny

1 paź 21:31
Mila:
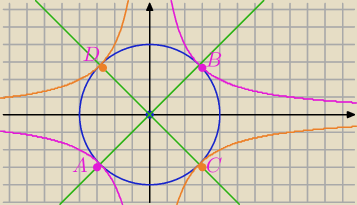
x
2+y
2=16
y=x i y=−x
Punkty przecięcia:
x
2+x
2=16
x
2=8
1) y=x
| | a | | a | |
A: x=2√2 i y=2√2 wtedy: y= |
| ⇔2√2= |
| ⇔a=8 |
| | x | | 2√2 | |
=========
lub
B: x=−2
√2 i y=−2
√2
a=8
2) y=−x
| | a | |
x=2√2 i y=−2√2 wtedy: −2√2= |
| ⇔a=−8 |
| | 2√2 | |
C i D punkty styczności
========
II sposób
x
4−16x
2+a
2=0
x
2=t>0
t
2−16t+a
2=0
Δ=0
Δ=256−4a
2
4a
2=256
a
2=64
a=8 lub a=−8
=========================
1 paź 21:31
Janek191:

1 paź 21:34
Dawid: Dziękuję bardzo !

1 paź 21:44

 ciekawe ...
ciekawe ...

 ... jasne
... jasne 

 x2+y2=16
x2+y2=16

