Zadanie.trygonometria Pomocy. Szybko: Wykaz, że jeśli α , β należą (0, π/2) i cosα=1/7 i cosβ= 13/14 to α−β= π/3

Benny:

	4√3
sinα=
	7

	3√3
sinβ=
	14

cos(α−β)=cosα*cosβ+sinα*sinβ

	13		36
cos(α−β)=		+
	98		98

	1
cos(α−β)=
	2

	π
α−β=
	3

Ktoś na pewno poda lepszy sposób, ale na razie łap to

woźny: czyżby klasówka?

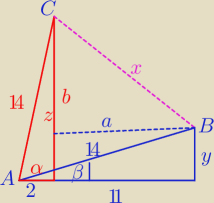Janek191: y² = 14² − 13² = 196 − 169 = 27 y = 3√3 −−−−− z² = 14² − 2² = 196 − 4 = 192 = 64*3 z = 8√3 więc a = 11 b = z − y = 8√3 − 3√3 = 5√3 dlatego x² = a² + b² = 11² + ( 5√3)² = 121 + 75 = 196 x = 14 ===== I AB I = 14 , I AC I = 14 i I BC I = x = 14

	π
więc Δ ABC jest równoboczny, czyli α − β = 60o =
	3

daras: @Pomocy. Szybko a kysz