[2 LO] Wykresy funkcji Desperat3001: Wyznacz wszystkie wartości parametru m, dla których równanie: a) (x + 3)² = m + 1 ma dwa rozwiązania ujemne

	5 − m
b) |x − 3| − 2 =		ma dwa rozwiązania dodatnie.
	4

olekturbo: a ) Δ > 0 x₁x₂ > 0 x₁ + x₂ < 0

Desperat3001: Nie rozumiem.

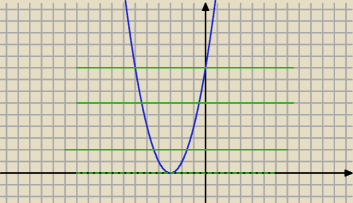
henrys: można i tak f(x)=(x+3)² f(0)=3²=9 dla 0<m+1<9 mamy dwa rozwiązania ujemne czyli dla −1<m<8

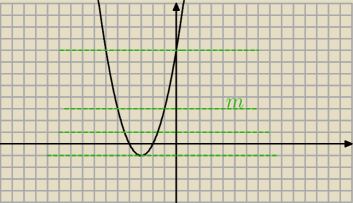
henrys: albo f(x)=(x+3)²−1 f(0)=8 dla −1<m<8 mamy dwa rozwiązania ujemne

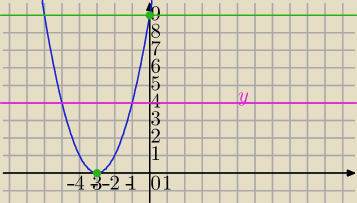
Mila: 1) Rozwiązujemy graficznie: 1) f(x)=(x+3)² 2) y=m+1 Dwa rozwiązania ujemne dla y=m+1∊(0,9) (różowa prosta przecina wykres w dwóch punktach o ujemnych wsp. x−owych) 0<m+1<9 /−1 −1<m<8

Desperat3001: Dziękuję, a b)?

Mila: Spróbuj narysować wykres funkcji f(x)=|x−3|−2 i takie samo rozumowanie przeprowadź, jeśli Ci nie wyjdzie, to napisz, narysuję.

Desperat3001: Fajnie by było, bo w odpowiedziach wychodzi m = (1,13) i nie wiem skąd to 13 się wzięło.

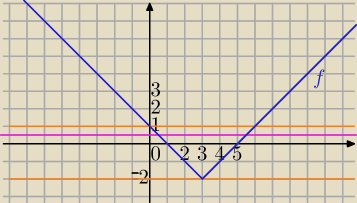
Mila: Możesz przesuwać prostą poziomą od (−2) do góry aż do 1. Wtedy masz przecięcie wykresu w dwóch punktach , ( patrz różowa prosta), których pierwsza wsp. jest dodatnia. ⇔

	5−m
−2<		<1 /*4
	4

−8<5−m<4 /−5 −13<−m<−1 /*(−1)⇔13>m>1⇔ 1<m<13

Desperat3001: Już wszystko jasne, dzięki.

Mila: