wyznacz wartości parametru a Zadaniowiec: Witam, czy te obliczenia są poprawne? Wyznacz te wartości parametru a, dla których zbiorem rozwiązań nierówności jest zbiór liczb rzeczywistych (a−1)x²+x+0,25≥0 zał: Δ ≥0 a>0 1−4(a−1)*0,25 ≥ 0 1−4(0,25a−0,25) ≥ 0 1−a+1 ≥ 0 −a ≥ −2 /:(−1) a ≤ 2

Metis: Czemu a>0 ?

Metis: I czemu Δ≥0 ?

Zadaniowiec: teraz to już sam do końca nie wiem, pogubiłem się trochę w tym. no tak, Δ nie może być ≥ 0, bo nie może przecinać osi OX chyba?

Zadaniowiec: dla a=1 jest x≥ −0,25, więc odpada chyba za długo już dziś siedzę przy tym, bo poprzednie tego typu zadania lepiej mi się liczyło, a teraz mi się myli

pigor: ..., obliczenia może i są (nie sprawdzałem) , ale warunki nie, otóż (a−1)x²+x+0,25 ≥0 dla ∀x∊R ⇔ a−1>0 i Δ=1²−4(a−1)*0,25< 0 ⇔ ⇔ a>1 i 1−a+1< 0 ⇔ a>1 i a<2 ⇔ a∊(1;2). ...

Metis: Najpierw rozpatrujesz przypadek dla a=1 Wtedy masz: x+0,25≥0 I komentarz, że dana nierówność nie jest spełniona przez wszystkie liczby R. Teraz należy zając się funkcją kwadratową: (a−1)x²+x+0,25≥0 Zatem a−1>0 ⇔ a>1 i Δ≤0. Wszystko pięknie widać z wykresu.

Mila: 1) a−1=0 wtedy masz równanie liniowe x+0.25=0 i ma rozwiązanie x=−0.25<0 nie odpowiada warunkom zadania. 2) a−1≠0⇔a≠1 (a−1)x²+x+0.25≥0 Wykres paraboli leży nad osią OX, ale może mieć jeden punkt wspólny (wierzchołek z osiąOX)⇔ a>1 i Δ≤0

	1
Δ=1−4*(a−1)*		=1−(a−1)=1−a+1
	4

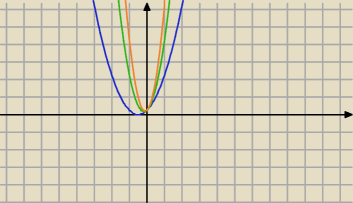
2−a≤0⇔ 2≤a i a>1⇔a≥2 Narysuję kilka wykresów: a=2 ⇔f(x)=x²+x+0.25 a=4 ⇔f(x)=3x²+x+0.25 a=6⇔f(x)=5x²+x+0.25

Zadaniowiec: dziękuję za tak dużą ilość wskazówek teraz wychodzi mi tak, więc raczej dobrze wszystko a−1>0 −−> a>1 Δ ≤ 0 1−4(4a−4)*0,25 ≤ 0 1−(a−1) ≤ 0 1−a+1 ≤ 0 −a ≤ −2 a ≥ 2 a∊ <2, +∞) jeszcze jutro na spokojnie sobie przejrzę to co mi tutaj doradziliście

pigor: ... , przepraszam, za swoje coś nie tak ...