ostroslupy
Monika:
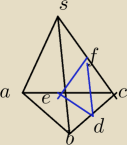
Witam, czy móglby mi ktos pomoc w rozwiazaniu tego zadania.
Ostroslup prawidlowy trojkatny o krawedzi podstawy a przecieto plaszczyzna przechodzaca przez
srodki krawedzi wychodzacych z wierzcholka C. Pole otrzymanego przekroju jest rowne S.
Wyznacz obiętość tego ostroslupa. Proszę o pomoc.
28 wrz 19:50
Kacper:

28 wrz 19:56
Monika: czemu zawdzieczam ten usmiech? wiem, ze rysunek nie jest dobry ale jestem w tym kiepska,
postaram sie zaraz narysowac dokladnie, nie wiem jak zaczac to zadanie, co trzeba po kolei
liczyc?
28 wrz 19:58
Monika:
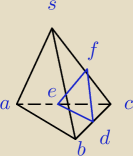
28 wrz 20:01
sushi_gg6397228:
1. odcinek łączący środki boków np |ED| =.... |AB|
2. pole trojkąta EFD= ...pole trójkąta ABS
3. liczysz wysokość trójkąta ABS , mając pole i krawędź podstawy
4. mając bok trójkąta ABC, policz długość odcinka np AO, gdzie O środek podstawy
5. Pitagoras trójkąt AOS −> H bryły
6. pole podstawy trójkąt ABC
7. V bryły
28 wrz 20:06
Bogdan:
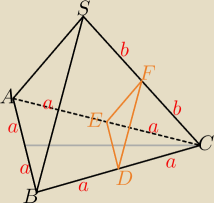
Jaka jest skala podobieństwa trójkątów ABS i DEF?
Jak się mają do siebie objętości brył podobnych?
28 wrz 20:07
Monika: |ED|=2|AB|
skala podobieństwa ABS i DEF to 2:1
objętości brył podobnych to też wyjdzie ABS dwa razy większa niz DEF?
28 wrz 20:18
Monika: Pole ABS to będzie 2S?
28 wrz 20:19
PW: Znajomość teorii się kłania. Na płaszczyźnie kwadraty o boku a i boku 2a są podobne, a stosunek
ich pól nie jest 1:2, ale 1:4.
Jak będzie z sześcianami?
28 wrz 20:21
Bogdan:
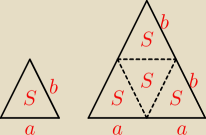
28 wrz 20:22
Monika: 1:8
28 wrz 20:24
Monika: Czyli pole ABS to 4S a wysokość ABS to 8S/a
28 wrz 20:28
Monika: nie wiem jak zrobic 4 punkt
28 wrz 20:34
sushi_gg6397228:
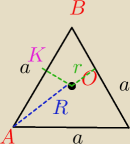
trójkąt równoboczny− podstawowe własności
punkt 4. miało być KO, a nie AO; wtedy
punkt 5. trójkąt KOS, a nie AOS
28 wrz 20:40
28 wrz 20:47
sushi_gg6397228:
W ZADANIU musisz trzymać się jednych oznaczeń; poprzedni rozmówca podał |AB|=2a
28 wrz 20:57
Monika: nic nie rozumiem
28 wrz 20:58
sushi_gg6397228:
masz 3 lata
u mnie |AB|=a, u Bogdana |AB|=2a
28 wrz 21:04
Monika: niestety nie mam odpowiedzi do tego zadania
28 wrz 22:25
Mila:
W takim razie przelicz, czy nie mam pomyłki w rachunkach.
28 wrz 22:26
Monika: dobrze, bardzo dziękuję

a h to nie powinno byc 8S/a?
28 wrz 22:34
Mila:
.
To przelicz , ja też przeliczę. Właśnie inna metodą liczyłam i nie zgodziły mi się wyniki.
28 wrz 22:49
Mila:
Napisz teraz swój wynik po tej poprawce.
28 wrz 22:54
Monika: wszystko tak samo tylko zamiast 192 bedzie 768
28 wrz 23:20
Mila:
Tak , zaraz napiszę, jeszcze raz, może komuś się przyda.
28 wrz 23:32
Mila:
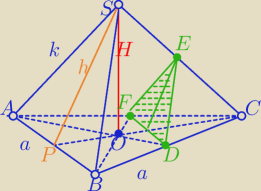
a− krawędź podstawy
S=P
ΔDEF
Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa⇔
P
ΔABS =4*P
ΔDEF=4S
ΔABS:
| | 1 | |
Porównanie pól: |
| *a*h=4S |
| | 2 | |
W ΔPOS:
h
2=|OP|
2+H
2
| | 64S2 | | a2 | |
H2= |
| − |
| /*12a2 |
| | a2 | | 12 | |
12a
2*H
2=64*12*S
2−a
4
12a
2*H
2=768S
2−a
4
| | 1 | | a2√3 | | √768S2−a4 | |
Vo= |
| * |
| * |
| |
| | 3 | | 4 | | 2√3*a | |
=============
28 wrz 23:38
 Witam, czy móglby mi ktos pomoc w rozwiazaniu tego zadania.
Ostroslup prawidlowy trojkatny o krawedzi podstawy a przecieto plaszczyzna przechodzaca przez
srodki krawedzi wychodzacych z wierzcholka C. Pole otrzymanego przekroju jest rowne S.
Wyznacz obiętość tego ostroslupa. Proszę o pomoc.
Witam, czy móglby mi ktos pomoc w rozwiazaniu tego zadania.
Ostroslup prawidlowy trojkatny o krawedzi podstawy a przecieto plaszczyzna przechodzaca przez
srodki krawedzi wychodzacych z wierzcholka C. Pole otrzymanego przekroju jest rowne S.
Wyznacz obiętość tego ostroslupa. Proszę o pomoc.


 Jaka jest skala podobieństwa trójkątów ABS i DEF?
Jak się mają do siebie objętości brył podobnych?
Jaka jest skala podobieństwa trójkątów ABS i DEF?
Jak się mają do siebie objętości brył podobnych?

 trójkąt równoboczny− podstawowe własności
trójkąt równoboczny− podstawowe własności
 a h to nie powinno byc 8S/a?
a h to nie powinno byc 8S/a?
 a− krawędź podstawy
S=PΔDEF
a− krawędź podstawy
S=PΔDEF