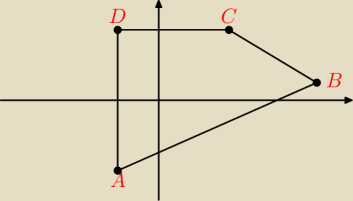
 Dany jest czworokąt ABCD , gdzie : A ( −1,−2 ) , B ( 8 , 1 ) , C ( 114 , 254 ) ,
D ( −1 , 254) ( rysunek obok ) . Oblicz odległości punktu S od boków tego czworokąta ,
jeśli:
a) S ( 2 ,4 ) , b) S ( 2 , 2 ) .
Dany jest czworokąt ABCD , gdzie : A ( −1,−2 ) , B ( 8 , 1 ) , C ( 114 , 254 ) ,
D ( −1 , 254) ( rysunek obok ) . Oblicz odległości punktu S od boków tego czworokąta ,
jeśli:
a) S ( 2 ,4 ) , b) S ( 2 , 2 ) .
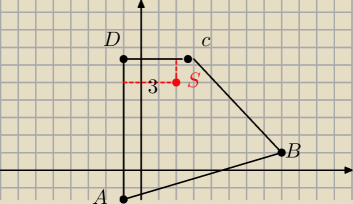 Odległość punktu S od prostej AD d(S,pr. AD)=3
Aby obliczyć odległość punktu S od prostej AB napisz równanie tej prostej i zastosuj wzór na
odległość punktu od prostej
Odległość punktu S od prostej AD d(S,pr. AD)=3
Aby obliczyć odległość punktu S od prostej AB napisz równanie tej prostej i zastosuj wzór na
odległość punktu od prostej
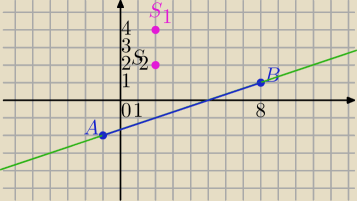 1) od AD i DC oblicz sam
2) Od boku AB
Piszesz równanie prostej przechodzącej prze punkty A i B.
A ( −1,−2 ) , B ( 8 , 1 )
y=ax+b
−2=a*(−1)+b
1=8a+b
========odejmuję stronami
−3=−9a
1) od AD i DC oblicz sam
2) Od boku AB
Piszesz równanie prostej przechodzącej prze punkty A i B.
A ( −1,−2 ) , B ( 8 , 1 )
y=ax+b
−2=a*(−1)+b
1=8a+b
========odejmuję stronami
−3=−9a
| 1 | ||
a= | ||
| 3 |
| 1 | ||
y= | x+b | |
| 3 |
| 1 | ||
−2= | *(−1)+b | |
| 3 |
| 5 | ||
b=− | ||
| 3 |
| 1 | 5 | |||
y= | x− | /*3 | ||
| 3 | 3 |
| |3*2−3*4−5| | |−11| | 11√10 | ||||
D(S1,k)= | = | = | ||||
| √12+32 | √10 | 10 |