równanie trygonometryczne onaaa: Rozwiąż równanie sin2x=−1/2 dla x∊<0;2π> Coś nie wyszło. Ja to zrobiłam tak: sin2x=−1/2 (2x=−π/6+2kπ lub 2x=7/6π+2kπ) i k∊C (x=−π/12+kπ lub x=7/12π+kπ) i k∊C Dla k=0 (x=−π/12 lub x=7/12π) i x∊<0;2π> ⇒ x=7/12π Dla k=1 (x=11/12π lub x=19/12π) i x∊<0;2π> ⇒ x=11/12π lub x=19/12π Dla k=2 (x=23/12 lub x=31/12π) i x∊<0;2π> ⇒ x=23/12π a więc moja odp. to x∊{7/12π; 11/12π; 19/12π; 23/12π} a w książce jest tylko x∊{7/12π; 11/12π}

Aga1.: Nie widzę błędu.

onaaa: w odpowiedziach jest x∊{7/12π; 11/12π}

Eta: Może ma być : x∊<0, π>

onaaa: na stronce jest tak samo jak w odp https://matematykaszkolna.pl/strona/2509.html

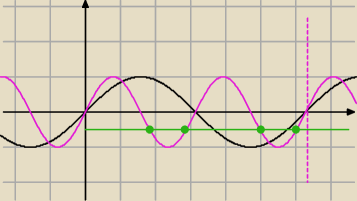
onaaa: z rysunku odczytam, że odp jest dobra, ale ja chciałam to spróbować moim sposobem "obliczeniowym" i mi jakoś nie wychodzi

PW:

	1
Jeżeli x∊[0, 2π], to 2x∊[0, 4π]. Prosta y = −		przecina wykres funkcji sinus
	2

rozpatrywanej na przedziale [0, 4π] w czterech punktach, a więc co do liczby rozwiązań masz rację.

Aga1.: Ale w Twoich obliczeniach nie zauważyłam błędu. Sprawdź jeszcze raz treść zadania.

PW: Na stronie jest inne równanie:

	1
sinx = −
	2

Eta:

	1
Na stronce jest sin(x)= −		dla x∊<0,2π> −− dwa rozwiązania
	2

	1
a w Twoim zad. : sin(2x)=−		dla x∊<0,2π> −− cztery rozwiązania
	2

chyba,że x∊<0,π> −−− wtedy będą dwa rozwiązania

onaaa: Sprawdziłam i polecenie jest ok. Jest to zadanko z "jak zdać maturę na poziomie rozszerzonym" Dariusza Kulmy

onaaa: To musi być błąd w książce. Dzięki wszystkim za pomoc

Eta: Na maturze będziesz znać odpowiedzi? nie ( no i fajnie bo podasz sama poprawną odpowiedź

PW: To jaki jest tytuł tej książki? Jak nie zdać matury na poziomie rozszerzonym? Jestem paskudny, bo zajmowałem się przygotowaniem komputerowym książek do druku i wiem jak łatwo o pomyłki.