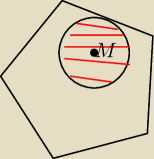
figury geometryczne 4max: Uzasadnuj ze punkt M lezacy wewnątrz wielokąta (punkt wewnwnetrzny) charakteryzuje nastepujaca wlasnosc : Istnieje kolo o srodku M cale zawarte w wielokącie

PW: Jeżeli punkt M należy do kąta i nie należy do jego ramion (niezależnie od tego, czy jest to kąt wypukły, czy wklęsły), to istnieje koło o środku M zawarte w tym kącie. Taka własność kąta pewnie była wcześniej udowodniona. Wielokąt jest częścią wspólną n kątów. Jeżeli powyższą własność kątów zastosujemy n razy i wybierzemy najmniejszy promień r spośród n promieni wskazanych dowolnie dla n kątów, to koło o środku M i promieniu r będzie zawarte we wszystkich n kątach, czyli w ich części wspólnej. Napisz uprzejmie: z podręcznika jakiego autora korzystasz?

4max: PW Te wlasnosci nie byly wczesniej udowadniane Podrecznik to Matematyka klasa 1 Jan Anusiak

PW: Koszmar. Słyszałem (od samego autora), że Anusiak jest zwolennikiem intuicyjnego podejścia do podstawowych zagadnień. Zwolenników precyzyjnych dowodów pilnujących aksjomatów, definicji i ścisłości pojęć nazywał pogardliwie "podstawiaczami".

4max: To w takim razie co proponujesz do nauki geometrii ?

Eta: Czyżby "małolat" ? i jego ulubiony .... Anusiak

henrys: Dla każdego punktu wewnętrznego M, danego wielokąta ustalamy najmniejszą odległość d tego

	1
punktu od brzegu wielokąta. Istnieje zatem takie r równe np.		d, że koło o promieniu r i
	2

środku w M w całości jest zawarte wielokącie.

PW: Nie wiem. Nie jestem ekspertem od dydaktyki, ale wątpię w sensowność prowadzenia takich rozważań przez ucznia pierwszej klasy. Nie wierzę również, żeby uczeń był w stanie skutecznie takie dowody przeprowadzać i w ogóle widział potrzebę takich dowodów. 90% uczniów powie: − Przecież to oczywiste, czego pani od nas chce? Przykładowe dzisiejsze pytanie: Czy zbiór jednopunktowy jest wypukły? może być ćwiczeniem przy rozważaniach logicznych, ale uczeń pierwszej klasy pewnie jeszcze tej logiki nie miał, więc pytanie jest dla niego "głupie", albo odpowie błędnie. Nigdy w życiu tej "wiedzy o wypukłości punktu" nie wykorzysta. Nie katuj się tymi zadaniami.

Mila: Popieram, od dawna to radzę koledze. Taka teoria zniechęci każdego ucznia I klasy LO do matematyki.