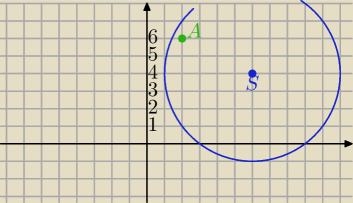
X Psychopata: Pytanie teoretyczne Okrąg o środku w punkcie (6,4) i promieniu 5 Jest wpisany w ten okrąg trójkąt równoboczny gdzie jeden wierzchołek jest równy (2,6) Czy jest wierzchołek B taki że B(x,6) ? Jak tak, to dlaczego? Proszę o wytłumaczenie.

henrys: (x−6)²+(y−4)²=25 Punkt (2,6) nie należy do tego okręgu (2−6)²+(6−4)²=16+4=20≠25

Mila: Równanie okręgu: (x−6)²+(y−4)²=25 Nie ma to sensu bo wierzchołek leży wewnątrz okręgu. Współrzędne wierzchołków Δ muszą spełniać równanie okręgu, bo Δ jest wpisany w okrąg. Podstaw wsp. punktu P=(2,6) do równania okręgu.

Psychopata: Chodziło mi o promień = 2√5 Ok treść zadania: W okrąg o środku S(6,4) wpisano trojkąt równoboczny ABC, którego jednym z wierzchołków jest pkt A(2,6). Oblicz współrzędne pozostałych wierzchołków. Pytanie jest analogiczne, czy jeden bok będzie równoległy do osi X i jak tak, dlaczego?

Mila: Niekoniecznie, jest kilka metod rozwiązania zadania, w wektorach orientujesz się? Prosta AS jest prostopadła do boku BC. Jeśli sobie nie poradzisz , to pisz, odpowiedz na pytanie o wektorach.

Psychopata: Spróbuję ale jakoś wieczorem może bo teraz idę na dwór xd

Psychopata: Znam się na wektorach znam kąt między wektorami warunki na wektory równoległe i prostopadłe no i informacje o wektorach na płaszczyźnie i w układzie współrzędnych więc jak mówisz że wektorami się da zrobić to myslę że sobie poradzę

Mila:

J: Bez wektorów: Znając promień okręgu , łatwo obliczysz bok a szukanego trójkąta:

	2		3*r		a√3		2h
r =		*h ⇔ h =		i dalej : h =		⇔ a =
	3		2		2		√3

teraz piszemy równanie okręgu o środku A(2,6) i promieniu a , punkty przecięcia tego okręgu i danego, są wierzchołkami szukanego trójkąta