kolokwium MaćkoZBogdańca: Wiem, że może wymagam zbyt dużo, ale kolokwium się zbliża, a ja jestem słaby z teorii zbiorów i elementów logiki. 1. Udowodnić następującą implikację B∩C=∅ ⇒ (A\C) ∪B=(A∪B) \ C 2. Niech: A= {(x,y) ∈ R² : |x| +x= |y| +y} , B= {(x,y) ∈ R² : |x| + |y| ≤2} , C= {(x,y) ∈ R² : |x + y| ≤1} . Wyznaczyć zbiory: A, B, C, A∪B, B∩C, A\C . 3. Czy zdanie złożone ∀ x∈R ∃ y∈R [xy=0 ⇒ x²+y²=0] jest prawdziwe? 4. Czy zdanie złożone ∀ x∈R ∃ y∈R [x² + x > −1 ⇒|x² − 1| > x² + 1] jest prawdziwe? 5. Udowodnić, że ∑(n,k) = 1 x 1 / k² ≤ 2 − 1 / n dla odpowiednich wartości n 6. Niech A= {x: x=a+b {7} , a,b∈Q} . Udowodnić, że ∀ x ∈ A ( xy ∈ A ∧ x⁻¹ =1 / x ∈ A) dla odpowiednich wartości n .

daras: a kolokwium w niedzielę rano ?

MaćkoZBogdańca: nie, ale muszę przyjrzeć się tym zadaniom, żebym wiedział jak je zrobić podobne na kolokwium

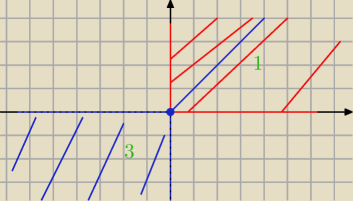
Aga1.: Zad. 2. a IyI+y=IxI+x Rozpatrujesz 4 przypadki .Zbiór A to suma rozwiązań. 1.Dla x≥0 i y≥0 ( zaznaczyłam na czerwono) mamy 2y=2x y=x .Częścią wspólną jest półprosta o początku w (0,0) przechodząca przez (1,1) (rozwiązanie na niebiesko) 2. x<0, y≥0 2y=0 y=0 Zaznacz w układzie współrzędnych 3.x<0 i y<0 −y+y=−x+x 0=0 4.x≥0 i y<0 x=0 zaznacz

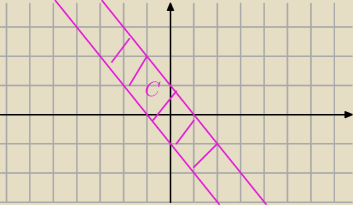
Aga1.: C można wyznaczyć dużo szybciej Ix+yI≤1 −1≤x+y≤1 x+y≤1 i x+y≥−1 y≤−x+1 i y≥−x−1