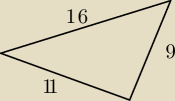
Planimetria majster: Korzystając z danych na rysunku oblicz: a) Miarę największego kąta b) Pole trójkąta c) Długość dwusiecznej najmniejszego kąta, zawartej w tym trójkącie. Najpierw obliczyłem pola ze wzrou Herona (obw 36) i wyszedł wynik √2268 Miarę największego kąta też obliczyłem − wyszło α=106^o Ale nie umiem obliczyć długości dwusiecznej najmniejszego kąta, zawartego w tym trójkącie

Qulka: (16/3)²=16²+x²−2•16•x•cosβ (11/3)²=11²+x²−2•11•x•cosβ więc (16/3)²=16²+x²+16•((11/3)²−11²−x²)/11

majster: A dlaczego tak? Dlaczego mnożymy pierwszy wzór z tw. cosinusów przez drugi?

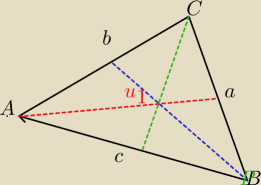
5-latek: A,B,C −katy trojkata a,b,c, boki trojkata u₁− odcinek dwusiecznej kąta A od wierzchołka A do boku a p−polowa obwodu

	2bc		A		2
u1=		*cos		=		√b*c*p(p−a)
	b+c		2		b+c

Patrz teraz na wzor na u₁ i napisz sobie wzory na dlugosc u₂ i u₃

5-latek: czyli dlugosc dwusiecznej niebieskiej i zielonej (bo nie podpisalem Sprawdz na swoim rysunku ktora to bedzie dlugosc i policz

prosta: można zbudować proporcję: 1. (16/3)²=16²+x²−2•16•x•cosβ (11/3)²=11²+x²−2•11•x•cosβ 2. 2•16•x•cosβ =16²+x²−(16/3)² 2•11•x•cosβ=11²+x²−(11/3)² 3. po podzieleniu równań stronami otrzymujemy:

	2•16•x•cosβ		162+x2−(16/3)2
		=
	2•11•x•cosβ		112+x2−(11/3)2

czyli

	162+x2−(16/3)2		16
		=
	112+x2−(11/3)2		11

liczby (11/3) oraz (16/3) to długości odcinków, na jakie dwusieczna podzieliła bok o najkótszej długości

Qulka: nie mnożyłam wzorów tylko podstawiłam jedną niewiadomą, żeby policzyć to co Cię interesuje https://matematykaszkolna.pl/strona/3778.html

majster: A mógłby ktoś wytłumaczyć dlaczego po podzieleniu boków przez dwusieczną wychodzą liczby 11/3 i 16/3 ?

prosta: liczby 11/3 i 16/3 otrzymamy z tw. o dwusiecznej https://matematykaszkolna.pl/strona/498.html

qulka: z twierdzenia o dwusiecznej https://pl.wikipedia.org/wiki/Twierdzenie_o_dwusiecznej_k%C4%85ta_wewn%C4%99trznego_w_tr%C3%B3jk%C4%85cie