Planimetria: Oblicz długości przekątnych, boku rombu i pole rombu Solitude1: W rombie cosinus kąta ostrego jest równy 1/4, a suma długości przekątnych wynosi √3 + √5. Oblicz: a) długości przekątnych i boku rombu b) pole rombu Czy jedna przekątna wynosi √3, a druga √5, czy niekoniecznie?

===: Pobaw się twierdzeniem cosinusów

wmboczek: niekoniecznie cos2α=1/4 tgα=d₁/d₂ √3+√5=d₁+d₂

Solitude1: Niczego nie rozumiem

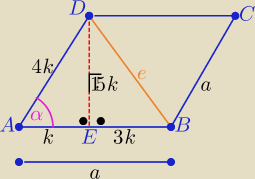
Eta: |BD|=e , |AC|=f −−− długości przekątnych rombu

	1		k
cosα=		=		, k>0
	4		4k

to wΔAED |AE|=k i |AD|=a=4k i |DE|=h=√(4k²)−k²= √15k i |EB|=3k w ΔEBD : e²==15k²+9k² ⇒ e²=24k² ⇒ e=2√6k= 2√2*√3k oraz w każdym rombie: e²+f²=4a² ⇒ f²=4a²−e² ⇒ f²= 64k²−24k² to f²=40k² ⇒ f= 2√10k= 2√2*√5k z treści zadania: e+f=√3+√5 ⇒ 2√2*√3k+2√2*√5k= √3+√5

	√2
to 2√2k=1 ⇒ k=
	4

zatem e= 2√2*√3*k = ..... = √3 i f= 2√2*√5*k=.....= √5

	e*f
P=		=......
	2

Solitude1: Bardzo dziękuję Ci Eta