pole czworokąta xxx: Pomoże ktoś? Nie wiem jak zrobić, kombinuje i nic z tego nie wychodzi 2.Rozpatrujemy równoległoboki, których obwód jest równy 16 cm, a kąt ostry ma miarę 45 stopni. b) wyznacz długości boków równoległoboku, który ma największe pole. Oblicz to największe pole. Ma wyjść a = 4, a pole 8√2 ktoś naprowadzi?

J: A to nie było Twoje ? : https://matematykaszkolna.pl/forum/299713.html

xxx: tak, tylko teraz przykład b), ale w tym a to wyszedł mi tylko drugi przypadek, w tym pierwszym przypadku popełniłam błąd w obliczeniach i dlatego wyszło mi 4. bo terz jak liczyłam to mi wyszło to samo a to nie wiem jak zrobić. pomożesz?

J: P = a*b*sinα 2a + 2b = 8 ⇔ a + b = 8 ⇔ b = 8 − a

	√2		√2
P = a(8 − a)8		= (−a2 + 8a)*
	2		2

pole będzie maksymalne, gdy nawias bedzie miał najwiekszą wartość ... dasz rade dale j ?

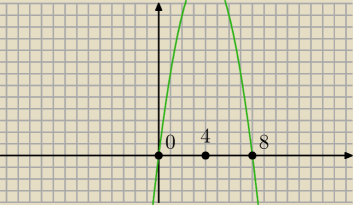
J: Tutaj masz pomoc

J:

	√2
ta ósemka przed		.. wpisana niechcący, zamiast: *
	2

xxx: nic z tego nie wychodzi

Nuti: @xxx Na rysunku @J widać (i można to oczywiście wyliczyć ze wzoru na wierzchołek paraboli), że pole jest maksymalne dla a równego 4. Podstaw więc a=4 do wzoru, który @J dla Ciebie wyprowadził o 20:29 (ostatnia linia wzorków w tamtym poście, P=...) − wstaw tam a=4 i otrzymasz maksymalne pole P.

Nuti: Jest tylko jeden problem, to pole wychodzi... ujemne, bo −16+32 jest ujemne

Nuti: Już widzę, gdzie nastąpiła pomyłka: w obliczeniach z 20:29 w drugiej linii 2a+2b=8, to a+b=4 a nie 8 (przeoczono osiem przy dzieleniu). Popraw tam i licz dalej tak samo jak @J.

J: (−a² + 8a) − to funkcja kwadratowa, która posiada maksimum lokalne.Jej miejscami zerowymi są punkty: a = 0 lub a = 8 (popatrz na wykres ). Funkcja ta osiaga maksymalna wartość dla : a = a_w , gdzie a_w to współrzędna wierzchołka paraboli ,która znajduje się w środku pomiedzy miejscami zerowymi ( patrz wykres) a_w = 4 , zatem ta funkcja osiaga największą wartość dla a = 4 Zatem maksymalne pole będzie wtedy,gdy: a = 4 i b = 4

Nuti: @J przeoczyleś 8 podczas dzielenia, stąd ujemny wynik.

J: Ja tam się pomyliłem ... 2a + 2b = 16 , stąd: a + b = 8 (popatrz na treść zadania)

Nuti: A! Patrzyłam tylko na ostatnią część, bo zakładałam, że to tam @xxx czegoś nie rozumie... Ale nadal masz P mniejsze od 0 dla a równego 4...

Nuti: Sorry, to ja krzywo odejmuję...

J:

	√2
jakim cudem ? P = ( −16 + 32)*		= 8√2
	2

Nuti: Pomyliłam się, przepraszam. Chyba źle spałam i widzę na krzyż

J: Nie przejmuj się ... liczymy skomplikowane całki i równania różniczkowe, a często mylimy się przy najprostszych rachunkach , a przynajmniej ja ...

Nuti: Dzięki za miłe słowo