Pochodne Kawa: Wyznacz liczbę pierwiastków równania w zależności od wartości parametru m. X²/x² + 4x + 4 = m Mam prawie zrobione lecz moge miec gdzieś błąd...

Kawa: Poprawka 2x²/x²+4x+4

J: Założenie: x² + 4x + 4 ≠ 0 ⇔ x² = m(x² + 4x +4) ⇔(1−m)x² −4mx + 4m = 0 ... i teraz dyskusja 1) 1 − m = 0 2) 1 − m ≠ 0

Kawa: Hm ja ładnie rysuje funkcje jak w poprzednim zadaniu z pochodnych.

Kawa: Mam asymptoty pozioma równa 2 i pionowa równa −2. I wiem jak rośnie w przedziałach z miejscami zerowymi −2 i 0. I założenie ze x≠−2. Jest ok?

J: po Twojej poprawce... ⇔ (2 − m)x² − 4mx − 4m = 0

J: Przecież polecenie w zadaniu jest zupełnie inne

Kawa: No ale z wykresu da sie to odczytać.

Kawa: Tylko nie czaję bo funkcja rośnie w przedziale (0 do nieskończoności) wiec mi sie nie zgadza.

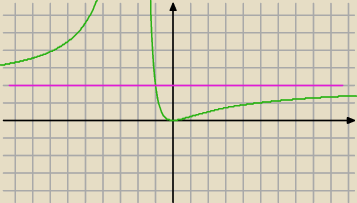
J: Graficznie: analizuj w ilu miejsca prosya: y = m przecina wykres w zależności od m

Kawa: Aha ok dzięki

PW: Kawa, skoro jesteśmy dalej w temacie "Pochodne", to może autor zadania chciałby widzieć badanie funkcji

	x2
f(x) =
	(x+2)2

− i po narysowaniu wykresu f oraz "kreski" y = m opowiadanie o liczbie punktów wspólnych dla obu wykresów w zależności od m. Oczywiście J proponuje lepsze rozwiązanie elementarne, ale zakładam, że masz ćwiczyć zastosowania pochodnej.

PW: Znowu jestem po czasie.

Kawa: Chociaż skad wiesz ze wykres z lewej jest nad asymptota pozioma...?

PW: Ta różowa kreska u J to nie jest asymptota, tylko wykres y = m.

Kawa: No dobra nieważne, pewnie poprostu liczysz wartości funkcji xd

J: Tak jak napisał PW .. .skoro to dział pochodne ... to trzeba badać tą funkcję

Kawa: A nieskończoność przez 0 daje?

Kawa: Tak z innej beczki.