Ciag arytmetyczny tworzy trojkat prostokatny Kuba: W trójkącie prostokątnym a,b,c tworzą ciąg arytmetyczny. A+b+c=42 Dochodzę do momentu w ktorym obliczam że b jest równe 14 ale wtedy wychodzi mi że inne wyrazy są równe albo 0 albo są równe b co mam zrobić?

3Silnia&6: 0<a<b<c a+b+c = 42 a² + b² = c² a = b −r b = b c = c + r a+b+c = 42 ⇒ 3b = 42 , b = 14 (14−r)² + 14² = (14 + r)² ⇒ r = ...

3Silnia&6: c = b + r* r − roznica ciagu aryt.

Eta:

	7
L=42 ⇒ 12r=42⇒ r=
	2

	21		28		35
a=		, b=		, c=
	2		2		2

	21		28		35		84
Sprawdzamy: a+b+c=		+		+		=		=42 ok
	2		2		2		2

	441		284		1225
a2+b2=c2 ⇒		+		=		ok
	4		4		4

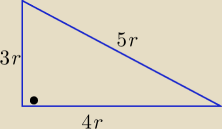
3Silnia&6: Dlczego a,b,c = 3r,4r,5r ?

J: bo suma 5 + 4 + 3 = 12 jest wielokrotnością: 42

PW: Trójkąt egipski?

ICSP: Kolega pyta dlaczego prawdziwa jest implikacja : boki trójkąta prostokątnego tworzą ciąg arytmetyczny ⇒ boki trójkąta są w stosunku 3:4:5 Niby oczywiste, ale uzasadnienie wypada przedstawić

J: moje ...żadne ( widziałem 48 )

PW: ICSP, dla ucznia wcale nie oczywiste, dlatego pytanie 3!=6 było uzasadnione. Może opowiedz, skąd się to bierze.

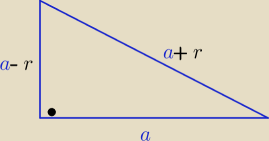
Eta: Uzasadniam (rys1) teraz mamy dane jak na (rys .2) r∊(0,a) z tw. Pitagorasa : (a−r)²+a²=(a+r)² ⇒ a²−4ar=0 /: a>0 stąd a−4r=0 ⇒ a= 4r to b= a−r= 3r , c= a+r= 5r i wszystko jasne Trójkąt prostokątny, którego boki tworzą ciąg arytmetyczny jest trójkątem egipskim o bokach długości : 3r, 4r, 5r , r>0

3Silnia&6: dzieki

Eta: