graniastosłupy ewela: Podstawą graniastosłupa prostego jest trójkąt równoramienny . przekątne ścian bocznych graniastosłupa tworzą z krawędziami podstawy kąty 30stopni 30 stopni i 45 stopni Oblicz objętość tego graniastosłupa jeśli jego wysokość jest równa 4

Nuti: Objętość graniastosłupa to wysokość razy pole S tego nieszczęsnego trójkąta w podstawie. Wysokość to 4, więc trzeba znaleźć pole S, bo: V = 4*S Łatwo wyliczyć z funkcji trygonometrycznych boki trójkąta w podstawie. Graniastosłup jest PROSTY, a to znaczy, że jego ściany boczne są prostopadłe do podstawy i możemy wyliczyć boki podstawy z odpowiednich trójkątów prostokątnych na ścianach bocznych.

	4
Dwa boki podstawy mają długość		=4√3 (4 to wysokość graniastosłupa, a więc i
	tg30

„pionowa" krawędź ścian bocznych − jeśli postawimy graniastosłup na podstawie, jak należy), a trzeci ma długość 4 (jest drugą przyprostokątną trójkąta o przyprostokątnej 4 i kącie 45 stopni). Mając długości trzech boków (4√3, 4√3 i 4) z pewnością jakoś umiesz policzyć jego pole. Są różne wzory. W najgorszym razie możesz policzyć sinus któregoś z kątów albo zastosować wzór Herona (jest straszny).

Nuti:

	α		2		√3
sin(		)=		=
	2		4√3		6

	√3		α
sinα=2*		*cos(		) − wylicz z jedynki trygonometrycznej i będziesz miała sinα
	6		2

	1
Pole S to		*4√3*4√3*sinα
	2

Nuti: Mój trójkąt jest BARDZO nieproporcjonalny! 4√3 jest dużo większe niż 2!

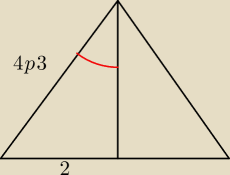
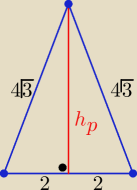kojot: h_p=√(4√3)²−2² = √48−4=√44=2√11

	1		1
Pp=		a*h=		*4*2√11= 4√11
	2		2

to V=P_p*H = 16√11 [j³]

Nuti: @kojot Jasne, brawo! Alem się wygłupiła

Eta: