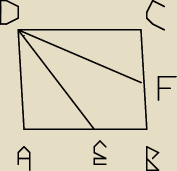
planimetrza: twierdzenie sinusów i cosinusów grudka: Z wierzchołka kąta ostrego rombu poprowadzono dwa odcinki dzielące ten romb na trzy części o równych polach. Oblicz długość każdego z tych odcinków, jeżeli bok rombu ma długość a,a kąt ostry ma miarę α. a=6 α=60 wyszło mi że f=g = √52+24√3

pigor: ..., niech ABCD − romb na na rys powyżej, to z jego symetrii i warunków zadania :∡D|=|∡B|=α − ostry, |∡A|=|∡B|=180^o−α i dla skrócenia zapisu |DE|=|DF|=x=?, oraz |AE|=y, wtedy −−−−−−−−−−−−−−−−−−−−−− P_DAE= ¹₃P_ABCD ⇒ ¹₂a*ysin(180^o−α)= ¹₃a²sinα / *²_a ⇒ ⇒ ysinα= ²₃asinα /:sinα>0 ⇒ y=²₃a, no to z tw. cosinusów dla ΔDAE : x²= a²+y²−2aycos(180^o−α) ⇒ ⇒ x²= a²+⁴₉a²+2a*²₃acosα ⇒ x²= ¹³₉a²+⁴₃a²cos60^o ⇒ ⇒ x²= ¹³₉a²+⁴₃a²*¹₂= ¹³₉a²+²₃a²= ¹⁷₉*6² ⇒ ⇒ x= ⁶₃√17 ⇒ |DE|= |DF|= 2√17. ...

grudka: a nie 2√19? [13+2*3] : [9] ...

Aga1.: Powinno być 2√19

Nuti: @grudka Dobrze sobie poradziłaś z rysunkiem, ale dla ułatwienia (gdybyś kiedyś jeszcze przysyłała zadanka na forum) podpowiem Ci, że w edytorze „rysuję" można kliknąć na symbol literki („T") i wtedy, gdy klikniesz w wybrane miejsce na rysunku, pojawi się tam kursor i możesz pisać literki z klawiatury, nie musisz ich sama produkować. Jedynym problemem jest to, że można pisać tylko jedną literkę za jednym kliknięciem, ale na ogół (np. w Twoim zadaniu) to wystarcza. Gdy chcesz napisać więcej literek lub cyfr koło siebie (np. długość boku 32), musisz po prostu kliknąć dwa (lub więcej) razy. Twój obrazek jest w każdym razie doskonale czytelny, chciałam Ci tylko podsunąć łatwiejszą metodę pisania na przyszłość