Oblicz pole czworokąta Solitude1: Dany jest równoległobok ABCD, w którym AB=2AD, a przekątne mają długość 2√2 i 4√2. Oznaczamy środki boków DC i BC odpowiednio jako punkty P i Q. a) Oblicz pole równoległoboku ABCD. //zrobiłem i wyszło 2√7 b) Oblicz pole czworokąta ABPQ //Kompletnie nie wiem jak je obliczyć, dlatego liczę na Waszą pomoc

Nuti:

	1
A jak obliczyłeś pole? Jest np. wzór		*2√2*4√2*sinα, gdzie α jest kątem ostrym między
	2

przekątnymi. Znalazłeś ten kąt (jak?) czy liczyłeś pole jakoś inaczej?

Solitude1: Z tw. cosinusów dla trójkąta ASB i BSC wyznaczyłem b = 2. Dzięki temu udało mi się wyznaczyć

	3
cosα =		. Z "Jedynki trygonometrycznej" wyznaczyłem sinusa = √7/4
	4

Nuti: Jeżeli masz pole P równoległoboku (czego ja nie widzę...), to pole czworokąta ABPQ jest łatwo, bo to jest (przez K oznaczyłam środek boku AB a przez O środek równoległoboku, czyli punkt przecięcia jego przekątnych)

	1		1		1		5
PΔ(PQO)+PΔ(AKP)+P(OQBK)=		P+		P+		P=		P.
	8		4		4		8

Nuti: S to środek? Ja oznaczyłam O... Zaraz się przyjrzę Twojej odpowiedzi.

Nuti: O, zapomniałam o istnieniu twierdzenia cosinusów

Nuti: Przeliczyłam pole wg Twojej metody i otrzymuję taki sam wynik. Zgadzasz się z moim rozwiązaniem b?

Solitude1: Powiem szczerze, że nic z tego nie rozumiem. Próbuję i próbuję i nadal nie wiem, skąd wzięły się te ułamki. Nie wiem czy dobrze zrobiłem rysunek.

Nuti: Zaraz narysuję. Ale widzisz, że równoległobok KBQO jest czwartą częścią całości? Trójkąt OQP jest połową takiej ćwiartki (OQCP). No i tórjkąt AKP jest połową rombu AKPD, który jest połową równoległoboku.

Solitude1: Tak, widzę

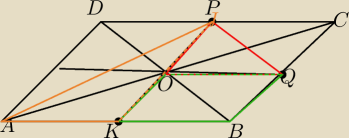
Nuti: Jasne?

Nuti: YES!

Nuti: Patrzyłeś mi przez ramię, gdy rysowałam?

Solitude1: Dobra, ogarnąłem. Dzięki