Okrąg i czworokąt. anaisy: Przekątne czworokąta ABCD, wpisanego w okrąg o środku S przecinają się w punkcie P. Niech v(XY) oznacza wektor o początku w X i końcu w Y. Udowodnij, że jeśli v(PA)+v(PB)+v(PC)+v(PD)=2*v(PS) to przekątne czworokąta ABCD są prostopadłe.

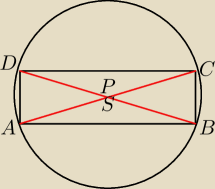
Nuti: To nie jest prawda. Kontrprzykład na rysunku. S=P, czyli prawa strona równania to wektor zerowy. Lewa też jest wektorem zerowym, bo wektory „znoszą się" parami. A prostopadłości przekątnych nie ma. Czy może źle zrozumiałam treść zadania?

anaisy: Nuti racja, dziękuję za wskazanie nieścisłości. Miało być jeszcze założenie, że punkty P i S nie pokrywają się.