Przekształcenia wykresów funkcji wykładniczej/logarytmicznej Koleszko: Mam pytanie. Dlaczego szkicując funkcję wykładniczą f(x) = 2^1−x + 2 mogłem zamienić(bo rozwiązanie dobrze wychodziło, w innych przypadkach też) na f(x) = 2^−x+1 + 2 Natomiast z funkcją logarytmiczną np. f(x) = log₂(−2−x) nie mogę zamienić na f(x) = log₂(−x−2), tylko aby wyszedł poprawny wynik muszę wyłączyć −1 przed nawias i dopiero wtedy zabrać się za szkicowanie wykresu funkcji ?

J: przecież: 1− x , to to samo co: −x +1

Koleszko: Tak, dlatego przy funkcjach wykładniczych było to poprawne. Jednak przy funkcjach logarytmicznych wychodzą dwa całkiem inne wykresy funkcji np. f(x) = log₂(−2−x), zamieniając na f(x) = log₂(−x−2) podczas szkicowania wykresu funkcji ze względu na −2 rysujemy asymptote pionową w punkcie x=2 (przesuwamy o dwa w prawo) i względem niej odbijamy w płaszyźnie OY wykres funkcji, natomiast mając f(x) = log₂−(x+2) szkicujemy asymptote pionową x=2 (w lewo przesuwamy o 2) i przez "−" odbijamy tak samo, jednak wychodzą całkiem inne dziedziny i rozwiązania. Drugie rozwiązanie jest prawidłowe według odpowiedzi do zadań.

PW: Co ty opowiadasz? − 2 − x = − x − 2, więc nie może być innego wykresu (nawet mi się nie chce czytać, gdzie popełniasz błąd w myśleniu o wykresach).

J: Troszkę zbładziłeś ... mamy narysować funkcję f(x) = log₂(−2− x) ⇔ f(x) = log₂(−x − 2) ⇔ ⇔ f(x) = log₂[−(x + 2)] . .. teraz rysujemy funkcję: f(x) = log₂x , przesuwamy o wektor [−2,0] czyli w lewo o 2 ( asymptota jest w punkcie x = −2, a nie x = 2 jak napisałeś) i odbijamy symetrycznie wzgledem tej asymptoty

J: i zauważ,że u Ciebie w poście 21:15 rozważasz: f(x) = log₂(−x − 2) oraz f(x) = log₂[−(x+2)], a to przecież jest ta sama funkcja

Koleszko: Rozumiem, tylko czemu trzeba ten minus wyciągnąć przed nawias aby poprawnie narysować wykres funkcji logarytmicznej ? Bo rysując f(x) = log₂(−x−2), rysuję sobie pomocniczą f(x)=log₂(x−2) przesunięty o dwie jednostki w prawo i f(x)=log₂(−x−2), czyli ten sam odbity względem osi OY tak jak przy np. f(x)=2^−x−2. Przy funkcjach wykładniczych nie musiałem wyciągać tego minusa przed nawias tylko rysowałem f(x)=2^x, przesuwałem o 2 jednostki w prawo f(x)=2^x−2 i następnie odbijałem względem osi OY i dostawałem wykres funkcji f(x)=2^−x−2

J: Muszę kończyć ..... jutro spróbuję Ci to bardziej wyjaśnić

Koleszko: Okej, mam nadzieję, że jest na to jakieś proste wytłumaczenie.

Koleszko: Pomoże ktoś ?

ZKS: Przecież rysując sobie funkcję f(x) = log₂(x − 2) i następnie, jeżeli odbijesz ją o oś OY to otrzymasz funkcję f(x) = log₂(2 − x), a nie f(x) = log₂(−x − 2).

ZKS: Pomyliło mi się. Rysując funkcję f(x) = log₂(x − 2) i odbijając ją teraz o oś OY otrzymasz f(x) = log₂(−x − 2).

ZKS: 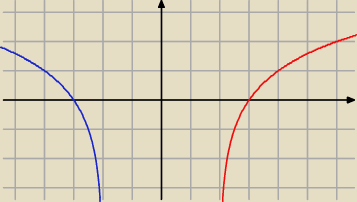y = log₂(x − 2) y = log₂(−x − 2)

Koleszko: Jaka ta matematyka lubi być podchwytliwa. Chyba już zrozumiałem mój błąd. Nie odbijałem wykresu funkcji względem osi OY tylko względem narysowanej asymptoty arrr.... Dziękuję Ci bardzo za pomoc !