stereometria
Gongini: Podstawą graniastosłupa prostego jest romb o boku 10 dm i kącie ostrym 30 stopni. Oblicz
długość przekątnych tego graniastosłupa, jeżeli jego wysokość ma 20 dm.
Muszę omówić jutro te zadanie przed klasa. Mógłby ktoś zrobić to zadanie albo chociaż opisać
krok po kroku jak to zrobić ? (prosiłbym o rysunek, wymagany

) Z góry dzieki.
21 wrz 20:12
Mila:
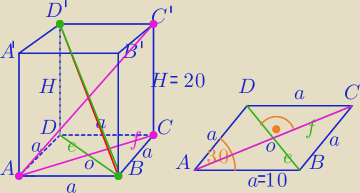
Dane:
a=10dm− długość boku rombu
H=20dm− wysokość graniastosłupa
α=30
0− miara kąta ostrego rombu
Szukane :
BD'−krótsza przekątna graniastosłupa
AC'− dłuższa przekątna graniastosłupa
W ΔACC' z tw. Pitagorasa :
|AC'|
2=f
2+H
2
W ΔDBD' z tw. Pitagorasa :
|BD'|
2=e
2+H
2
Trzeba obliczyć długości przekątnych rombu ABCD.
Znasz tw. cosinusów? Czy trzeba inaczej sobie poradzić?
21 wrz 20:34
Gongini: A skąd obliczyć dł. przekątnych e,f ?
21 wrz 20:46
Mila:
Właśnie pytam, czy znasz tw. cosinusów?
Jeśli nie miałeś na lekcjach to policzymy inaczej.
21 wrz 20:51
Gongini: Nie miałem jeszcze.
21 wrz 21:29
Mila:
21 wrz 21:29
Mila:
P
ABCD=a
2*sin30
0
P
ABCD =50 dm
2
Pole rombu możemy obliczyć z wzoru:
e*f=100
W ΔAOB: z tw. Pitagorasa
e
2+f
2=400
Masz układ równań :
e*f=100
e
2+f
2=400
−−−−−−−−−−−−−−−−−
Trzeba obliczyć e
2 i f
2 , aby podstawić do wzorów na przekątne graniastosłupa.
Spróbujesz sam?
21 wrz 21:41
Gongini: Tak, poradze już sobie. Dziękuje

21 wrz 21:42
Mila:
Jeśli będą kłopoty to pisz. Powodzenia.

21 wrz 21:45
Mila:
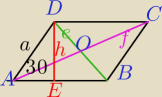
II sposób (łatwiejszy)
Obliczasz wysokość rombu:
P=a*h
10*h=50
h=5
====
W ΔAED:
AE=5
√3
|EB|=10−5
√3
W ΔDBE:
h
2+|EB|
2=e
2
5
2+(10−5
√3)
2=e
2
25+100−100
√3+25*3=e
2
e
2=200−100
√3
e
2+f
2=400
podstaw za e
2 i dokończ
21 wrz 21:59
Eta:
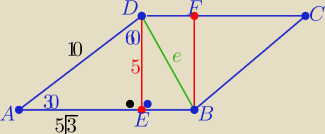
|DB|=e , |AC|=f |AD|=|AB|=10
f
2+e
2=4a
2 ⇒ f
2= 400−e
2
|EB|=10−5
√3 ⇒ |EB|=5(2−
√3)
z tw. Pitagorasa w trójkącie EBD :
e
2= 5
2+(5(2−
√3)
2 ⇒ e
2=25+25(7−4
√3) ⇒ e
2= 25(1+7−4
√3)
e2= 100(2−√3) to f
2=400−100(2−
√3) ⇒ f
2=100(2+
√3)
d
1, d
2 −−− długości przekątnych graniastosłupa o wysokości H=20
to d
12= H
2+f
2=...... i d
22= H
2+e
2=.....
................. dokończ
21 wrz 22:08
Gongini: Obliczyłem tym sposobem i wyszło, ale sytałem sie po klasie to jednak trzeba tymi funkcjami...
Mogłabyś to rozpisać za pomoca funkcji jak obliczyc e i f ?
21 wrz 22:13
Mila:
Jakimi funkcjami?
Masz mój sposób i Ety, chcesz z tw, cosinusów?
21 wrz 22:15
Mila:
Możesz zaprezentować wszystkie sposoby, bo są poprawne.
21 wrz 22:16
Gongini: Podobno wymagany z tw. cosinusów, mogłabyś zrobić ?
21 wrz 22:17
Mila:
Za chwilę.
21 wrz 22:21
Mila:
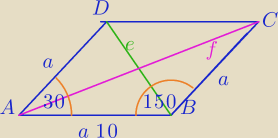
W ΔBAD: z tw. cosinusów:
e
2=a
2+a
2−2*a*a*cos(30
o)
e
2=200−100
√3
W ΔABC:
| | 1 | |
cos(150o)=cos(180−30)=−cos30=− |
| |
| | 2 | |
f
2=a
2+a
2−2*a
2*cos(150
o)
f
2=200+100
√3
|AC'|
2=f
2+H
2⇔
|AC'|
2=200+100
√3+20
2
|AC'|
2=600+100
√3=100*(6+
√3)
|AC'|=
√100*(6+√3)=10
√6+√3
Resztę oblicz sam.
21 wrz 22:38
 ) Z góry dzieki.
) Z góry dzieki.
 Dane:
a=10dm− długość boku rombu
H=20dm− wysokość graniastosłupa
α=300− miara kąta ostrego rombu
Szukane :
BD'−krótsza przekątna graniastosłupa
AC'− dłuższa przekątna graniastosłupa
W ΔACC' z tw. Pitagorasa :
|AC'|2=f2+H2
W ΔDBD' z tw. Pitagorasa :
|BD'|2=e2+H2
Trzeba obliczyć długości przekątnych rombu ABCD.
Znasz tw. cosinusów? Czy trzeba inaczej sobie poradzić?
Dane:
a=10dm− długość boku rombu
H=20dm− wysokość graniastosłupa
α=300− miara kąta ostrego rombu
Szukane :
BD'−krótsza przekątna graniastosłupa
AC'− dłuższa przekątna graniastosłupa
W ΔACC' z tw. Pitagorasa :
|AC'|2=f2+H2
W ΔDBD' z tw. Pitagorasa :
|BD'|2=e2+H2
Trzeba obliczyć długości przekątnych rombu ABCD.
Znasz tw. cosinusów? Czy trzeba inaczej sobie poradzić?


 II sposób (łatwiejszy)
Obliczasz wysokość rombu:
P=a*h
10*h=50
h=5
====
W ΔAED:
II sposób (łatwiejszy)
Obliczasz wysokość rombu:
P=a*h
10*h=50
h=5
====
W ΔAED:
 |DB|=e , |AC|=f |AD|=|AB|=10
f2+e2=4a2 ⇒ f2= 400−e2
|EB|=10−5√3 ⇒ |EB|=5(2−√3)
z tw. Pitagorasa w trójkącie EBD :
e2= 52+(5(2−√3)2 ⇒ e2=25+25(7−4√3) ⇒ e2= 25(1+7−4√3)
e2= 100(2−√3) to f2=400−100(2−√3) ⇒ f2=100(2+√3)
d1, d2 −−− długości przekątnych graniastosłupa o wysokości H=20
to d12= H2+f2=...... i d22= H2+e2=.....
................. dokończ
|DB|=e , |AC|=f |AD|=|AB|=10
f2+e2=4a2 ⇒ f2= 400−e2
|EB|=10−5√3 ⇒ |EB|=5(2−√3)
z tw. Pitagorasa w trójkącie EBD :
e2= 52+(5(2−√3)2 ⇒ e2=25+25(7−4√3) ⇒ e2= 25(1+7−4√3)
e2= 100(2−√3) to f2=400−100(2−√3) ⇒ f2=100(2+√3)
d1, d2 −−− długości przekątnych graniastosłupa o wysokości H=20
to d12= H2+f2=...... i d22= H2+e2=.....
................. dokończ
 W ΔBAD: z tw. cosinusów:
e2=a2+a2−2*a*a*cos(30o)
W ΔBAD: z tw. cosinusów:
e2=a2+a2−2*a*a*cos(30o)