funkcje trygonometryczne Dawid : 1. Punkt P należy do ramienia końcowego kąta α (alfa) a punkt Q− do ramienia końcowego kąta β (beta). Oblicz cos α + cos β. a) P(3,1), Q(−1,1/2) b) P(−2, pierwiastek z 2), Q(pierwiastek z 2/2, 1) 2. Wybierz dowolny punkt na ramieniu końcowym kąta alfa i oblicz wartości funkcji trygonometrycznych tego kąta. Bardzo proszę o pomoc, wytłumaczenie

Nuti: A co to jest „ramię końcowe"? Czy należy się domyślać, że „ramię początkowe" to dodatnia półoś osi X, a wierzchołek znajduje się w punkcie (0.0)? Jeżeli tak, to zrób rysunek, zaznacz co trzeba, znajdź cosα i cosβ z samej definicji tych punktów, podstaw i pododawaj. Zgłoś się w razie problemów!

Nuti: z definicji funkcji trygonometrycznej cosinus, a nie jakichś tam punktów, chyba mi ktoś klawiaturę przejął

Nuti:

	√5
a) −		jeżeli się nie pomyliłam i jeżeli dobrze zinterpretowałam (nieco niejasną)
	10

treść zadania.

Dawid : Niestety, ja też się zastanawiam nad tym..bo jest tak napisane ramię końcowe i tyle Niestety nie, bo wyniki są takie w książce: 3: a) 3√10−4√5/10 b) √3−√6/3 a do 4go nie mam odp

Dawid : znaczy zrobiłem tak, w 3a), tylko, że wyszło mi r=√4/5 i później jak liczę cosα: 0,5/√5/4 i dochodze do miejsca 2/5√5/4 i nie wiem co dalej, znaczy jak dodac cosα i cosβ, które wyszło mi √30/10. Dobrze? Wie ktoś?

Qulka: a) dla α r=√10 cosα3/√10 dla β r =√5/2 cosβ= −2/√5

	3−2√2
cosα+cosβ =		= jak odp po usunięciu niewymierności
	√10

henrys:

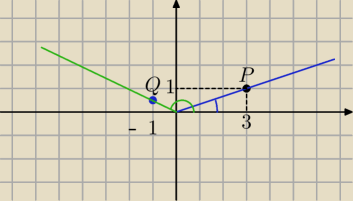
	3
cosα=		, r1=√32+12=√10
	r1

	3		3√10
cosα=		=
	√10		10

	−1		√5
cosβ=		, r2=√(−1)2+(1/2)2=√5/4=
	r2		2

	−1*2		−2√5
cosβ=		=
	√5		5

	3√10		−2√5		3√10		4√5		3√10−4√5
cosα+cosβ=		+		=		−		=
	10		5		10		10		10

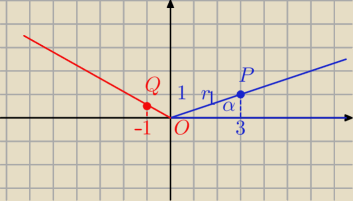
Janek191: a) r₁² = 3¹ + 1² = 10 r₁ = √10

	x		3
cos α =		=
	r1		√10

−−−−−−−−−−−−−−−−−−−−−−

	1		5
r22 = 12 + 0,52 = 1 +		=
	4		4

	√5
r2 =
	2

	x		−1		2
cos β =		=		= −
	r2		√5     2		√5

−−−−−−−−−−−−−−−−−−−−−

	3		− 2		3		2√2
cos α + cos β =		+		=		−		=
	√10		√5		√10		√10

	3 − 2√2		3 √10 − 2√20		3√10 − 4√5
=		=		=
	√10		10		10

I OP I = r₁ I O Q I = r₂

Qulka: b) dla α r=√6 cosα= −2/√6 =−√6/3 dla β r =√3/2 cosβ= 1/√3=√3/3

	√3−√6
cosα+cosβ =
	3

Eta:

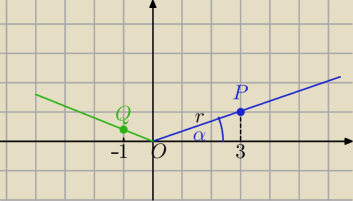
	x		3		3√10
a) cosα=		, r=|OP|= √32+12= √10 i x=3 ⇒ cosα=		=
	r		√10		10

	x		√5		x		−2		4√5
cosβ=		, r=|OQ|= √1+14=		⇒ cosβ=		=		= −
	r		2		r		√5		10

	3√10−4√5
to cosα+cosβ=
	10

Eta: Ejjj z Wami Spadam

Janek191: Ale wysyp ! Pozdrowienia dla Ety

Janek191: A Dawid ani be, ani me, ani kukuryku

Eta: Dawajmy więcej......... gotowców

Dawid : Dziękuję bardzo! Przepraszam, ale robię w między czasie inne lekcje i patrzę co jakiś czas, czy ktoś pomógł. W każdym razie jeszcze raz bardzo dziękuję. A o co chodzi z tymi gotowcami Bo nie rozumiem.. Nie można nie rozumieć zadania?

Qulka: można nie rozumieć ale wyjaśnianie zadania to co innego niż napisanie odpowiedzi ... tylko że na interreakcje zazwyczaj się nie doczekamy i kończy się na gotowcach