pole rownolegloboku ...: Dany jest rownoleglobok w ktorym dlugosci sasiednich bokow roznia sie o 3. Kat ostry ma miare 60°, a dluzsza przekatna ma dlugosc 3√7. Oblicz pole tego rownolegloboku i dlugosc krotszej przekatnej.

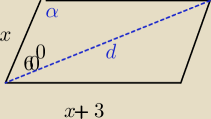
Aga1.: d=3√7 α=180⁰−60⁰ z twierdzenia cosinusów obliczysz boki d²=x²+(x−3)²−x(x−3)*cos120⁰ P=x*(x−3)*sin60⁰ Drugą przekątną jeszcze raz z tw. cosinusów

...: Pole ma byc 9√3 a dlugosc krotszej przekatnej 3√3

...: pomoze ktos ?

Aga1.: Trochę jest literówek , więc Ci pierwszą część rozwiążę

	1
cos1200=cos(180−60)=−cos600 =−
	2

Zgubiłam 2 w tw. i powinno być x+3 i x>0

	1
(3√7)2=x2+x2+6x+9−2x(x+3)*(−		)
	2

63=2x²+6x+9+x²+3x 3x²+9x−54=0 (można podzielić przez 3, ale nie dzieliłam)) Δ=81+4*3*54=729 √Δ=27

	−9+27
x1=		=3
	6

x₂<0 x+3=6

	√3
P=3*6*		=9√3
	2