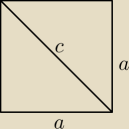
Niewspolmiernosc odcinkow 5-latek: Przerabiam teraz niewspolmiernosc odcinkow Twierdzenie : Przekatna kwadratu nie jest wspolmierna z jego bokiem Dowod : Jeśli przy wspolmiernosci odcinkow a i b mamy

	|a|		m
(1) |b|=m*		=		*|a| gdzie m in ∊C+
	n		n

to jeśli a jest bokiem kwadratu i c jego przekatna wiec na podstawie (1) powinno być

	m		m
(2)|c|=		|a| i		musi być ułamkiem nieskracalnym
	n		n

Z Pitagorasa mamy ze |c|²= |a|²+|a|²=2|a|² czyli mamy ze

m2		m2
	|a|2= 2|a|2 czyli		=2 czyli m2=2n2
n2		n2

Widac ze prawa strona jest liczba parzysta i żeby zachodzila rownosc to także m² musi być liczba parzysta Stad m jest liczba parzysta postaci 2k Wtedy m²=(2k)²=4k²=2n² wiec 2k²=n² Z tego wynika z eliczba n bylaby parzysta co nie jest możliwe bo m i n nie maja wspólnych

	m
dzielników (		jest nieskracalny wiec nie mogą się obie dzielic przez 2
	n

Udowdnilismy wiec ze przekatna kwadratu nie jest wspolmierna z jego bokiem czyli jeśli bok kwadratu a=1 to c=√2 i te odcinki sa niewspolnierne i ztego wynka ze licba√2 nie jest liczba wymierna Będę miał teraz kilka zadań z niewyniernosci liczb (nie lubie tych zadań gdzie pewnie ten dowod trzeba będzie wykorzystać Zadanie nr 1 Udowodnij ze 3√2 jest liczba niewymierna

Janek191: Niech

	m
3√2 =		, m, n ∊ ℕ
	n

	m2
9*2 =
	n2

3*3*2*n*n = m*m ; po rozłożeniu n oraz m na czynniki pierwsze, będzie po lewej stronie nieparzysta ilość 2 , a po prawej parzysta

5-latek: Dzieki Ci