Oblicz ∫_{k{ xydx + sinydy po brzegu trójkąta o wierzchołkach ryter: Bardzo proszę o pomoc! Oblicz ∫{k{ xydx + sinydy po brzegu trójkąta o wierzchołkach : A(−1,0) B(0,0) C(0,2) .

Nuti: Widzę, że poprawiłeś współrzędne trójkąta, ale niestety nie pamiętam, jak się takie paskudztwo liczy...

J: Juz Ci ktoś napisał, że to nie jest trójkąt

J: a .... poprawił

Nuti: Teraz już jest! To ja byłam

henrys: @ Nuti należy się za te piękne rozwiązania i podpowiedzi

J: a czy funkcję podcałkową też dobrze przepisałeś/aś ?

Nuti: Dzięki, @henrys, chociaż w tym przypadku moja pomoc nie na wiele się zdała Może jednak zajrzę do jakiegoś podręcznika do „calculusa"...

ryter: J. − tak, dobrze przepisałem.

Nuti: Sięgnęłam do (bardzo) starego i zapomnianego zeszytu ze studiów i chyba rozwiązałam! Nie gwarantuję poprawności. Zaraz zapiszę.

5-latek: Tylko jedna osoba na tym forum siega do zeszytow ze studiow . Wiec kochana Pani doktor niech Pani nie mowi ze to nie jest Pani

daras: https://www.youtube.com/watch?v=d8pIb8Xijcc

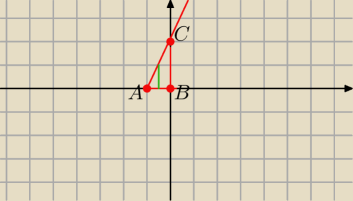
Nuti: Znalazłam zapomniane twierdzenie Greena. Zamienia całkę po krzywej na całkę powierzchniową. Nigdy jeszcze nie pisałam całek w tym edytorze. Mam nadzieję, że nie wyjdzie z tego jakaś masakra. Na obrazku obszar D znajduje się wewnątrz trójkąta ABC, a prosta AC ma równanie y=2x+2. K to krzywa (suma trzech odcinków). Widzę, że nie ma tu symboli do pochodnych cząstkowych, użyję więc literki d... Z twierdzenia Greena:

	dQ(x,y)		dP(x,y)
∫K (P(x,y)dx+Q(x,y)dy)=∫∫D (		−		)dxdy
	dx		dy

W Twoim przypadku P(x,y)=xy, a Q(x,y)=siny czyli

dP(x,y)		dQ(x,y)
	=x, a		=0
dy		dx

Podstawiamy wszystko do wzoru z twierdzenia Greena: Twoja całka po łamanej = ∫∫_D(0−x)dxdy=∫∫_D(−x)dxdy a to się równa, z twierdzenia Fubiniego (najpierw całkuję po y−ku dla każdego x, od 0 do 2x+2, jak pokazuje zielona kreseczka na rysunku, a później wszystko po x od −1 do 0. Trudno tu zapisać granice całkowania...): = ∫₋₁⁰(∫₀^2x+2(−x)dy)dx=∫₋₁⁰(−xy)|₀^2x+2)dx=∫₋₁⁰(−x(2x+2)−0)dx=

	2x3		−2		1
= ∫−10(−2x2−2x)dx=(−		−x2)|−10=0−(−		−1)=		.
	3		3		3

Mam nadzieję, że się nigdzie nie pomyliłam! Sprawdź szczególnie uważnie wszystkie minusy po ostatnim znaku równości, bo jest ich tak dużo, że łatwo się pomylić!

Nuti: @5−latek Dziecko, naprawdę mnie z kimś mylisz, Ty mnie na oczy nie widziałeś! Poza tym nikt do mnie nigdy nie mówił na pani...

Nuti: Myślisz, że ja mam jeszcze jakiś inny nick na tym forum? Otóż nie, jestem tu tylko jako Nuti, i to od bardzo niedawna. 2 tygodnie? Nigdy przedtem tu nie byłam.

Nuti: @Qulka, powiedz im, że nie jestem Tobą, bo mnie już ktoś pytał, czy Tobą jestem i pewnie @5−latkowi również o Ciebie chodzi (widziałam kiedyś, jak sięgałaś po zeszycik ).

5-latek: Nuti jasne jest ze Cie na oczy nie widziałem . Nawet gdbys była z mojej czy sąsiedniej miejscowości to skad mialbym wiedzieć. Skoro napisalas ze (bardzo starego) to mniemam z tego ze nie jesteś już dwudziestolatka tylko dorosla kobieta a do takiej zwracam się na Pani (tak mnie wychowano A to dziecko w następnym roku skończy 58lat

Nuti: @5−latek wyluzuj, do mnie naprawdę nigdy w życiu nikt na pani nie mówił... Bardzo dziwnie bym się czuła, gdybyś teraz zaczął. Chyba nie mam do Ciebie na pan?

ryter: Chyba wszystko okej, kojarzę wzór Greena. Dziękuję bardzo @Nuti

5-latek: Nuti OK Alez oczywiście ze nie . Zaraz będę wyjezdzal do pracy i jak wroce mam nadzieje ze będziesz mi pomagać w moich zadankach

5-latek:

Nuti: Ja często myślę, że Twoje zadanka są „tak dla jaj" i że tylko sobie z nas żartujesz...

Qulka: zdecydowaną większość zadań robię z głowy i na tempo, ale czasem pamięć zawodzi i sięgam po zeszyty jednakże nie jestem jedyną osobą która starannie prowadzi notatki i zachowuje je przez lata, więc zdecydowanie nie jest to wskaźnik i wyznacznik mnie jakbym miała zmieniać nick to raczej wrócę do aniabb, bo obecna zmiana wynikała z faktu, że po długiej przerwie zapomniałam jak się logowałam i absolutnie żadnych innych nie będę używać

Dobromir: powinno być "Qlka" bo wtedy jest bardziej stylowo. Przecież i tak to "u" tam będzie tak jak np. w słowie "Qszetka" albo "Qwejt"

Qulka: i wtedy będą do mnie mówić Olka

Dobromir: chyba tylko analfabeci grunt to być w dzisiejszych czasach trendi. Ja niestety z moim imieniem nie mam lekko

Qulka: wolę własną ścieżkę, a moda i trendy jak dla mnie za szybko się zmieniają ja mam swój świat zagadek logicznych http://www.conceptispuzzles.com/

ICSP: Wzór Grenna ma pewne założenia które trzeba sprawdzić przed zastosowaniem.