Podaj zbrór wartości a Stefan: √2 sinx+sinxcosx+√2 cosx=a

PW:

	1
Środkowy składnik to		sin(2x).
	2

	π		π
Dwa skrajne to sin		cosx + cos		sinx = ... (sinus sumy)
	4		4

:): Albo idąc w strone

1		1
	(sinx+cosx)2+√2(sinx+cosx)=a+
2		2

Nuti: Używałam tych samych wzorów co @PW (dwójka przed pierwszym sinusem, bo pierwiastki z 2 trzeba podzielić przez 2 żeby uzyskać sinus i cosinus 45 stopni) i z max jest łatwo, bo znajduję x, które bez wątpienia realizuje największą możliwą wartość wyrażenia, ale min? − nie jestem pewna.

	π		1
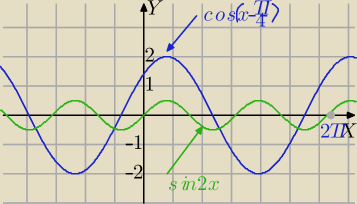
a(x)=2sin(x+		)+		sin(2x).
	4		2

	π		1
Wartość x=		daje jedynkę w obu sinusach, czyli wartość 2		jest bez wątpienia
	4		2

maksymalna. Jedynek nikt nie przeskoczy. Nie widzę jednak, jak (bezboleśnie) określić minimum.

PW: No tak, sie myśli, a sie nie pisze (mówię o sobie). Jeszcze raz: Po podzieleniu przez 2 mamy

	√2		1		√2		a
		sinx +		·2sinxcosx +		cosx =
	2		4		2		2

i teraz

	π		1		a
sin(x+		) +		(sin2x) =		,
	4		4		2

	π		a
maksymalne wartości obu składników dla x =		, czyli maksymalna wartość		jest równa
	4		2

	1
1 +		,
	4

a więc a_max = 2,5. Minimum też na razie nie widzę.

PW: Pomysł ; ) jednak lepszy

Nuti: chyba że po prostu brutalnie przyrównamy pochodną do zera, nie jest zbyt skomplikowana

	π
a'(x)=2cos(x+		)+cos(2x).
	4

Nuti: racja, bo można podstawić t za sumę i bada się kwadratowe...

Mila: MOże tak:

	1
f(x)=√2*(sinx+cosx)+		sin(2x)⇔
	2

	π		1
f(x)=2cos(x−		)+		sin(2x)
	4		2

	π		1
g(x)=2cos(x−		) i h(x)=		sin(2x) − funkcje ograniczone
	4		2

	π
−2≤2cos(x−		)≤2
	4

	1		1		1
−		≤		sin(2x)≤
	2		2		2

==================== Wartość najmniejsza:

	π
2cos(x−		)=−2⇔
	4

	π
cos(x−		)=−1⇔
	4

	π		1		5π		1		1
x=		+π wtedy h(π)=		sin(2*		)=		*sin(5π2)=
	4		2		4		2		2

	1		3
−2+		=−		− wartość najmniejsza f(x)
	2		2

−−−−−−−−−−−−−−−−−−−−−−−− Wartość największa:

	π
2cos(x−		)=2
	4

	π
cos(x−		)=1
	4

	π		1		π		1
x=		wtedy: h((x)=		sin(2*		)=
	4		2		4		2

	1
2+		=212 − wartość największa f(x)
	2

−−−−−−−−−−−−−−−−−−−−−−−−−−

	3		5
Zwf=<−		,		>
	2		2

Nuti: Wartość największą załatwiliśmy wcześniej (bezdyskusyjnie, o 7:49), a wartości najmniejszej nadal nie mamy. Pokazałaś, że wartość najmniejsza jest ≤ −1.5, ale nie udowodniłaś, że nie może być mniejsza od tej liczby. Nie mówię, że −1,5 nie jest minimum, mówię tylko, że tego nie dowiodłaś.

ICSP: Tworzę funkcję : f(x) = √2sinx+sinxcosx+√2cosx określoną : f : R → f(R) = D i szukam zbioru D

	1		1
f(x) = √2sinx + sinxcosx + √2cosx = √2(sinx + cosx) +		(1 + sin2x) −		=
	2		2

	1		1		1		3
=		(sinx + cosx)2+√2(sinx + cosx)−		=(		(sinx + cosx) + 1)2 −
	2		2		√2		2

	1
−√2 ≤ sinx + cosx ≤ √2 // *
	√2

	1
−1 ≤		(sinx + cosx) ≤ 1 // + 1
	√2

	1
0 ≤		(sinx + cosx) + 1 ≤ 2 // 2
	√2

	1		3
0 ≤ [		(sinx + cosx) + 1]2 ≤ 4 // −
	√2		2

	3		5
−		≤ f(x) ≤
	2		2

	3		5
D = [−		,		]
	2		2

PW: Tak, dlatego pisałem, że pomysł : ) z 22:44 jest dobry − ICSP zrealizował to z talentem

Mila: Ad.15:3

Mila: 15:31