zbiór Kiełbasy hihihi: Hej, wiem że to nie jest zadanko i pewnie troszkę nie na temat piszę, ale chciałam Was zapytać czy w zbiorze do Matematyki Kiełbasy jest analiza matematyczna? A jeśli tak to w której części?

RJS: Zapytaj się swojej Pani w szkole.

hihihi: dzięki RJS, naprawdę bardzo mi pomogłeś, nie spodziewałam się takiej wyczerpującej odpowiedzi, a no i tak pomocnej przede wszystkim

Eta: Geometria analityczna jest w cz. 2

RJS: Zawsze do usług a tak poważnie tom 1 zadanie 56−87 i zadanie 633 z tomu drugiego. Stron nie pamiętam.

Janek191: @ Eta Jej chodziło o analizę matematyczną

karolina: Zrobi ktoś ? 1. Podstawą ostrosłupa jest trójkąt równoboczny. Jedna z krawędzi bocznych ostrosłupa jest prostopadła do płaszczyzny podstawy. Uzasadnij, że ściana boczna leżąca naprzeciw tej krawędzi ma pole większe od pola każdej z pozostałych ścian bocznych ostrosłupa. 2.W ostrosłupie o podstawie kwadratowej odcinek SE jest wysokością ostrosłupa a punkt E jest srodkiem krawędzi AD. Oblicz miarę konta alfa, nachylenia ściany BCS do płaszczyzny, podstawy ostrosłupa oraz jego objętość V, gdy lASl=15cm i lBSl=17cm.

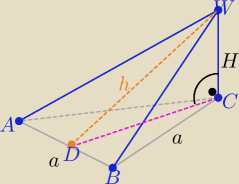Eta: 1/ h>H bo h jest długością przeciwprostokątnej w trójkącie prostokątnym DCW

	h*a		a*H
P(ABW)=		i P(BCW)=P(ACW)=
	2		2

	h*a		H*a
zatem		>
	2		2

c.n.u

hihihi: @karolina chyba pomyliłaś miejsce na zadanko, nie uważasz?! @dzięki Janek191 @Eta chodziło mi o analizę, ale mimo wszystko dziękuję

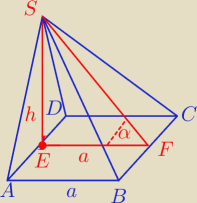Janek191: 2) I AS I = 15 cm I BS I = 17 cm = I CS I a = I AB I = I BC I = I CD I = I AD I Odcinek AS jest prostopadły do odcinka AB, więc z tw. Pitagorasa mamy 15² + a² = 17² a² = 17² − 15² = 289 − 225 = 64 więc a = √64 = 8 ============ oraz I EF I = a = 8 cm Δ AES jest prostokątny, więc z tw. Pitagorasa mamy h² + (0,5 a)² = I AS I² h² = 15² − 4² = 225 − 16 = 209 h = √209 cm ===========

	h		√209
tg α =		=		≈ 1,8071 ⇒ α ≈ 61o
	a		8

========== Objętość ostrosłupa:

	1		1		1		64
V =		Pp*h =		a2*h =		*82* √209 =		√209
	3		3		3		3

	64
V =		√209 cm3 ≈ 308,4 cm3
	3

===================

korob: Analiza jest w drugiej części.