nierowności dobrze robie dzieląc przez -2 czy 2
kamil: −2(x−1)(x+3)>0 /:−2
20 wrz 17:35
olekturbo: nie
robisz to zle
20 wrz 17:36
Metis: Jak chcesz to możesz sobie dzielić.
−2(x−1)(x+3)>0 /:(−2)\
(x−1)(x+3)<0
20 wrz 17:37
kamil: −2(x−1)(x+3) >0 /:2
(x−1)(x+3)>0
a teraz?
20 wrz 17:38
olekturbo: zmien znak
20 wrz 17:39
kamil: aha okej i wychodzi mi
x2+2x−3<0
delta wyszła 16 pierwiatek 4
x1=−3
x2=1
i nie wiem jaki jest wspołczynnik żeby ramiona paraboli dac w dol czy w gore?
20 wrz 17:39
Metis: Po co Δ ?
Masz postać iloczynową, z której od razu odczytuje się miejsca zerowe funkcji.
(x−1)(x+3)<0
x1= 1 v x2=−3
Rysujesz oś, parabole i teraz odczytujesz.
20 wrz 17:42
kamil: ale nie wiem czy ramiona maja byc w góre czy w dół ale chyba w dół bo a<0
20 wrz 17:43
Metis: Patrzysz na postać końcową:
(x−1)(x+3)<0
a=1
a>0
Parabola z ramionami do góry.
20 wrz 17:44
kamil: nie rozumiem ale gdzie ten wspolczynnik
20 wrz 17:45
5-latek: Ze wstydu uciekl sobie
20 wrz 17:47
kamil: co ?
20 wrz 17:47
kamil: 5−latek o co ci chodzi ?
20 wrz 17:48
Metis: −2(x−1)(x+3)>0 ⇒ (x−1)(x+3)<0
W obu przypadkach wyjdzie ten sam wynik...
20 wrz 17:48
kamil: nie rozumiem jak gdzie ten wspolczynnik jest czemu a>0
20 wrz 17:49
Metis: a(x−1)(x+3)<0
Jedynki się nie piszę, jest umowna.
a=1 zatem a>0.
Jeśli chodzi o postać:
−2(x−1)(x+3)>0
to a=−2, zatem a<0
20 wrz 17:50
kamil: ale metis to nie wiem z ktorego rysowac bo jak a>0 to ramiona do góry a jak a<0 ramiona w dół
20 wrz 17:52
Metis: Rysuj albo −2(x−1)(x+3)>0 albo (x−1)(x+3)<0 . Wynik będzie ten sam... Sprawdź.
(x−1)(x+3)<0 ⇔ −2(x−1)(x+3)>0
20 wrz 17:53
5-latek: Metis nie
W obu przypadkach wyjdzie ten sam zbior rozwiazan
ale wsppolczynnik a −2(x−1)(x+3)>0 to (−2x)*x=−2x2<0 czyli a<0 wiec ramiona skierowne
w dol
a wprzypadku (x−1)(x+3)<0 to x*x=x2 czyli a=1>0 i ramiona w dol
20 wrz 17:54
kamil: aha okej czyli ramiona do góry paraboli zaznaczylem −3 i 1 polaczylem parabolą do góry zbiór
roziwazan (−3:1) tak ?
20 wrz 17:56
5-latek:
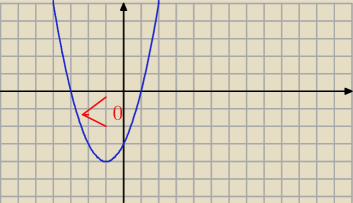
20 wrz 17:58
kamil: nie rozumiem jaki bedzie zbior rozwiazan w koncu , i jaki jest ten wspolczynnik a
20 wrz 18:03
Metis: Tak
5−latku , chodzi mi o ten sam zbiór rozwiązań. Jasnym jest, że wykresy funkcji beda
różne

20 wrz 18:04
ZKS:
5−latek chyba czegoś nie widzę, ale wydaje mi się to co napisał
Metis jest

.
20 wrz 18:06
5-latek: To ja zle zrozumialem

Mylalem ze napisales ten sam wspolczynnik , a TY napisales wynik
20 wrz 18:06
Metis: kamil a ty zapoznaj się z tym:
3413 , bo nie wiesz o czym prawimy.
20 wrz 18:12


 .
.
 Mylalem ze napisales ten sam wspolczynnik , a TY napisales wynik
Mylalem ze napisales ten sam wspolczynnik , a TY napisales wynik