Pomocy
Krzyś : Dziesiąty wyraz pewnego ciągu geometrycznego jest równy 10.Oblicz iloczyn 19 początkowych
kolejnych wyrazów tego ciągu.
a
10=10
aq
9=10
... pytanie co dalej...

20 wrz 15:12
Krzyś : a
10=10

20 wrz 15:12
daras: a pierwszy jaki

20 wrz 15:16
Krzyś : Nie ma podanego 1−szego

20 wrz 15:17
daras: to skąd wiesz, że to ciąg geom.


20 wrz 15:20
Krzyś : Z treści zadania

20 wrz 15:23
Kacper:
.
.
.
a
10=10
a
11=10*q
.
.
a
19=10*q
9
wymnożyć i napisać odpowiedź

20 wrz 15:25
daras: to rozwiąż ukł. r−ń:
a
1q
9 = 10
a
1a
1qa
1q
2...a
1q
18 =..chyba sie uda

20 wrz 15:27
Krzyś : Dziękuje

20 wrz 15:27
Eta:
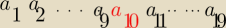
a
10=a
1*q
9=10 −−− wyraz środkowy
a
1*a
19= a
2*a
18= a
3*a
17=...= (a
1*q
9)
2 =10
2=
100
takich par iloczynów równych wyrazowi środkowemu a
10 w tym iloczynie jest
9
zatem iloczyn tych 19 wyrazów jest równy : 9*100=
900
20 wrz 15:28
daras: ..= 1019
jak się nazywa ta liczba ?
20 wrz 15:30
Eta:
Widzę ,że =
daras 
20 wrz 15:31
Kacper:
Eta coś mały ten Twój iloczyn

20 wrz 15:32
daras: η za mało jeszcze wypiła...kompotu

20 wrz 15:34
daras: to 10 trylionów
20 wrz 15:35
Eta:
No jasne , że pokićkałam

100*100*100*...100 *
10= 100
9*10= 10
19
Idę w takim razie po "kompot"

20 wrz 15:42
Eta:
Napisałam "takich par iloczynów jest 9" po 100 czyli 1009 i *środkowy
odp: 1009*10=1019
20 wrz 15:44
daras: tylko nie z gumijagód


20 wrz 15:44










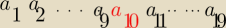 a10=a1*q9=10 −−− wyraz środkowy
a1*a19= a2*a18= a3*a17=...= (a1*q9)2 =102=100
takich par iloczynów równych wyrazowi środkowemu a10 w tym iloczynie jest 9
zatem iloczyn tych 19 wyrazów jest równy : 9*100=900
a10=a1*q9=10 −−− wyraz środkowy
a1*a19= a2*a18= a3*a17=...= (a1*q9)2 =102=100
takich par iloczynów równych wyrazowi środkowemu a10 w tym iloczynie jest 9
zatem iloczyn tych 19 wyrazów jest równy : 9*100=900



 100*100*100*...100 *10= 1009*10= 1019
Idę w takim razie po "kompot"
100*100*100*...100 *10= 1009*10= 1019
Idę w takim razie po "kompot" 

