Pochodne Kawa: Narysuj wykres funkcji f i wyznacz jej ekstrema. W których punktach funkcja ta nie ma pochodnej: F(x) = |1−x²|/1+x²

PW: Funkcja jest zdefiniowana wzorem

	x2 − 1
F(x) =		dla x∊ ...
	1 + x2

	1 − x2
F(x) =		dla x∊ ...
	1 + x2

Funkcja ta − jako iloraz dwóch funkcji różniczkowalnych i określonych na wszystkich z wyżej opisanych przedziałów (bez ich końców) − jest różniczkowalna wszędzie z wyjątkiem tych końców − tam różniczkowalność trzeba badać. Krótko mówiąc − trzeba badać istnienie pochodnej tam, gdzie wzór definiujący funkcję zmienia postać. Badać z definicji lub licząc pochodne lewo− i prawostronne.

Kawa: To znaczy liczę pochodna obu funkcji i potem jak je narysować?

J: wykresów pochodnych nie musisz rysować, masz narysować tylko wykres tej funkcji, a wskazówki dał Ci PW

Kawa: Liczę pochodne obustronne ale mi nie wychodzi nic fajnego bo mianownik sie nie zeruje a licznik tak. Co teraz?

J: Poczytaj dziewczyno kurwa jakieś książki, wszystkie rozwiązania oraz wskazówki dał Ci już kolega PW, nie ma co tutaj ślęczeć dalej nad tym.

J: kolego ...bądź tak uprzejmy i podszywaj się pode mnie

Kawa: Czemu sie denerwujesz? Z tym zadaniem jest kupa roboty i chce wiedzieć czy dobrze robię.

Kawa: Brak asymptoty pionowej?

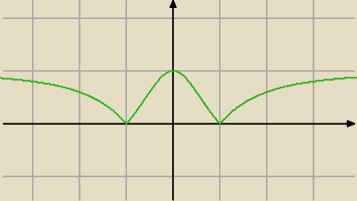
J: wpis 14:24 ...to wpis jakiegoś chama Ta funkcja nie ma asymptot pionowych , bo: D = R ,posiada asymptotę poziomą : y = 1, dwa minima lokalne f(1) = f(−1) = 0 i jedno maksimum lokalne: f(0) = 1 Nie jest różniczkowalna w punktach: x = −1 orax x = 1

J:

Kawa: No to idę dobrym tropem dzięki jak coś będę pytać.

Kawa: Dziękuje bardzo za pomoc wszystko rozumiem 😌

Kawa: I na przyszłość Panie J − nie denerwuj się tak proszę, jestem studentka, uczę się i nie wszystko jest dla mnie zrozumiałe. Kiedyś pewnie też dorosnę i będe pomagać innym osobom. Niestety, na razie muszę pytać innych. Także proszę o wyrozumiałość!

J: jeszcze raz Ci tłumaczę,że ten wpis z 14:34 , to nie mój post ( ktoś użył mojego "nicka" )

J: Pomagam na tym forum z dobrej woli, a nie z przymusu, więc denerwowanie się byłoby nieuzasadnone

Kawa: Nie znam się na tym, przepraszam. Tak radzę tylko na przyszłość, aby się wiecej uśmiechać!