rownania z parametrem
marek: pisze tutaj o pomoc, gdyż moja matematyczka (od rozszerzonej) ni w cholere nie potrafi
przekazać wiedzy potrzebnej do rozwiązania tych zadań. Nie proszę tutaj o gotowca już
zrobionego, tylko wytłumaczenie choć kilku przykładów, krok po kroku, co trzeba założyć, co
trzeba wiedzieć, co trzeba zrobić , żeby dać radę to rozwiązać !
Jednym słowem − z czym to się je, taka lekcja poza lekcją..
Dzięki z góry
polecenie brzmi: Wyznacz wartość parametru m, dla którego równanie z niewiadomą x ma co
najmniej jedno rozwiązanie.
a) mx+m=m
2x+1
b) x=m
x
c) (|m|−3)x=m+3
d) 2x=|m|(x+1)
e) mx−m
2=4m+4−2x
19 wrz 21:50
Qulka: wyznaczyć x = .... i zależnie od wyniku analizować
jak ułamek że mianownik ≠ 0 aby rozwiązanie
jeśli mianownik = 0 i licznik =0 to nieskończenie wiele (bo przed podzieleniem to było 0•x=0)
jeśli mianownik = 0 i licznik ≠0 to sprzeczne (bo przed podzieleniem to było 0•x= coś )
19 wrz 22:03
Mila:
a) mx+m=m
2*x+1 porządkujemy to równanie
m*x−m
2*x=1−m równanie liniowe
x*(m−m
2)=1−m
x*m*(1−m)=1−m
1) m*(m−1)≠0 ⇔m≠0 i m≠1 masz jedno rozwiązanie
2)m=0 to masz sytuację:
x*0*(−1)=−1 brak rozwiązania bo L=0 a P=−1
3) m=1 masz sytuację:
x*1*0=0 niezależnie od wyboru x równanie ma rozwiązanie bo L=0 =P
istnieje nieskończenie wiele rozwiązań.
19 wrz 22:08
Qulka: ogólnie to funkcja liniowa ( bo wszystkie x masz w pierwszej potędze ) więc sprowadza się do
ax+b=0 szukamy miejsc zerowych prostej
gdy a≠0 jedno rozwiązanie
gdy a=0 i b=0 nieskończenie wiele
gdy a=0 i b≠0 to sprzeczne
jak na rysunku
19 wrz 22:10
Qulka:
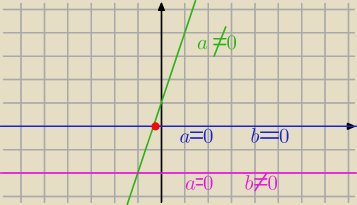
19 wrz 22:12
Bogdan:
"pisze tutaj o pomoc, gdyż moja matematyczka (od rozszerzonej) ni w cholere nie potrafi
przekazać wiedzy potrzebnej do rozwiązania tych zadań"
Oj nieładnie. To nie ktoś ma Ci przekazywać wiedzę do rozwiązywania zadań na poziomie
rozszerzonym, ale Ty sam masz tę wiedzę i umiejętności zdobywać poprzez samodzielne
ćwiczenia. Ty sam!. Wtedy osiągniesz sukces.
19 wrz 22:31
s: Tak a nauczyciel najlepiej niech popija kawe i nic nie robi, idąc tym tokiem myślenia po co w
ogóle tracić czas na szkoły jak można się wszystkiego samemu nauczyć?
Wiadomo że trzeba też samemu się uczyć w domu bo uczeń przyswojoną wiedze na lekcji( ile
przyswoi to też inna kwestia) zazwyczaj szybko zapomina i trzeba ją utrwalić, ale nauczyciel
jest od tego aby wiedze teoretyczną jak i poniekąd praktyczną przekazać.
20 wrz 09:30
.: a szkoła jest po to, aby tę wiedzę systematycznie przyswajać w małych kawałkach
bez tego przymusu nawet samouki by wyginęły

20 wrz 09:39
Kacper:
Nauczyciel przy takiej liczbie godzin w szkole jak to ma miejsce obecnie nie nauczy
rozwiązywania każdego zadania.
Trzeba włożyć trochę własnego wysiłku.
20 wrz 10:32
Janek191:

20 wrz 10:39
daras: ale to nie wszyscy rozumieją
marek np. woli wrzucic tu serię zadań a samemu miec wolny weekend

20 wrz 11:10
5-latek: Ja postuluje ;
wrocic do porzedniego systemu kształcenia ,gdzie nawet o szkoły chodzilo się w sobote i nikomu
to nie przeszkadzalo .
Przeciez na zaocznym czy wieczorowym kształceniu nauka tez odbywa się w sobote i niedziele i
nikt nie protestuje
20 wrz 12:06
PW: ... i więcej wf, najlepiej na 1., 2. i 3. lekcji,
20 wrz 12:10
5-latek: Popieram

20 wrz 12:17




