Równania prostych zawierających boki trójkąta. Robson Green: Wyznacz równania prostych zawierających boki trójkąta ABC, jeśli dane są równania dwóch prostych zawierających jego wysokości oraz współrzędne wierzchołka A. x+y=0 , y=3x, natomiast A= (7,−1)

wmboczek: A nie leży na tych wysokościach więc należy wyznaczyć: 1) prostopadłe do wysokości przechodzące przez A − 2boki 2) przecięcia tych boków z wysokościami − wierzchołki B i C 3) prostą BC − 3ci bok

Nuti: Zrób rysunek, to wyliczysz bez trudu. Pamiętaj, że prosta prostopadła do y=−x ma współczynnik

	1
kierunkowy 1, a prostopadła do y=3x ma współczynnik kierunkowy −		.
	3

Powodzenia!

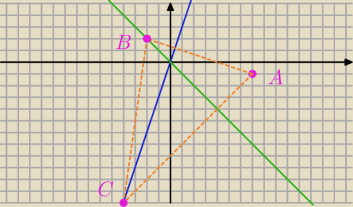
Qulka: AC y=−x−8 AB y=−x/3+4/3 BC y = 7x+16

Nuti: AC ma kierunkowy PLUS 1

Qulka: AC y=x−8

Nuti: Na rysunku dobrze, więc pewnie „przejęzyczenie" w spisywaniu.

Nuti: Resztę wyników mam tak samo, więc prawdopodobnie są prawidłowe, bo liczyłyśmy niezależnie

Qulka: ja tylko liczyłam kratki