Może ktoś zobaczyć czy jest dobrze? marta : Rozwiązaniem nierównosci |x−3| ≤7 jest przedział Ja to zrobiłam tak: |x−3|≤7 x−3≤−7 x≤−4 |x−3|≥7 x≥7+3 x≥10 (−∞,4> ∪ <10,∞)

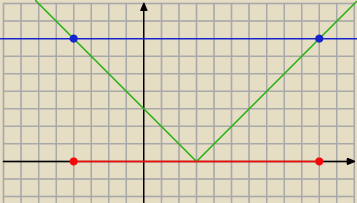
Qulka: zielona niżej niż niebieska jest od <−4;10>

Qulka: algebraicznie jak zdejmujesz moduł to nie zmieniasz znaku nierówności gdy dodatni czyli : x−3≤7 x≤10 a potem zmieniasz znak pod modułem −(x−3)≤7 więc x−3≥−7 x≥−4

Janek191: I x − 3 I ≤ 7 − 7 ≤ x − 3 ≤ 7 − 7 + 3 ≤ x ≤ 7 + 3 − 4 ≤ x ≤ 10 x ∊ < − 4 ; 10 > ===========

Mila: |x−3|≤7 Nierówność oznacza, że szukasz wszystkich liczb , których odległość na osi liczbowej od liczby 3 jest mniejsza niż 7jednostek lub równa 7 jednostek. Przedział możesz szybko ustalić tak: Liczba 3 jest środkiem szukanego przedziału: Patrz na oś⇒ x∊<−4,10> Metoda przydatna, jeśli jest krótki przedział.

marta: Dziękuje za pomoc