...
zorro: | | 3x | |
Wyznacz ekstrema funkcji f(x) = |
| |
| | x2+4x+4 | |
| | 3x | | 3x | |
f(x) = |
| = |
| Df=R\{−2} |
| | x2+4x+4 | | (x+2)4 | |
−3x
212=0
x = 2 V x = −2∉D
pytanie: jak teraz będzie wyglądał wykres, czy będzie na nim tylko 2, czy będzie też −2?
19 wrz 15:25
zorro:
w f(x) i f'(x) w mianowniku miało być 2 w potędze
zamiast −3x212 miało być −3x2+12
19 wrz 15:27
zorro: patrzyłem na wykres na wolframie i skłaniałbym się do tego aby było −2 i 2..
19 wrz 15:29
Janek191:
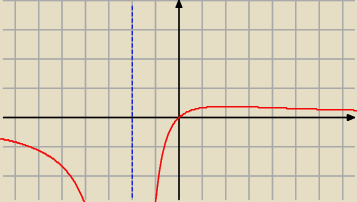
19 wrz 15:30
Janek191:

19 wrz 15:30
:): rysujesz tradycyjnie..a w tym punkcie −2, który nie należy do dziedziny liczysz granice prawo i
lewostronną (jest to −∞)
19 wrz 15:33
5-latek: A koń Zorra by wiedział

19 wrz 15:41
zorro:
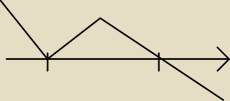
Może i koń by wiedział, ale ja nadal nie wiem

| | −3x2 + 12 | |
f'(x)= |
| zacząłem rysować od dołu bo jest minus, |
| | (x+2)4 | |
dalej idąc zaznaczyłem kolejno −2 i 2. −2 bo tam jest asymptota, a 2 bo wyszło z 'x'.
tam gdzie jest asymptota jakby odbijam, bo dalej musi isc do gory
to jest dobrze?
19 wrz 16:17
Janek191:
Do czego jest Ci potrzebny wykres pochodnej funkcji ?

19 wrz 16:21
zorro: Nie wiem jak Ty, ale ja eksrema wyznaczam tylko na podstawie wykresu, więc
dobrze byłoby go poprawnie rysować..
19 wrz 16:24
Janek191:
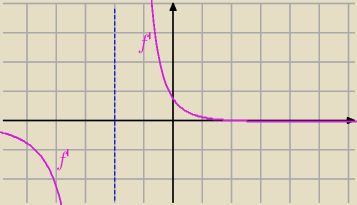
19 wrz 16:26
Janek191:
Wykres funkcji f − patrz. 15.30
Dla x = 2 f '(2) = 0 oraz pochodna zmienia znak z + na − , więc mamy maksimum
lokalne
| | 3*2 | | 6 | | 3 | |
ymax = f(2) = |
| = |
| = |
| |
| | ( 2 + 2)2 | | 16 | | 8 | |
19 wrz 16:29
Aga1.: f
'(x)>0
| −3x2+12 | |
| >0 dla x ≠−2 (x+2)4>0 |
| (x+2)4 | |
−3(x−2)(x+2)>0
19 wrz 16:31
zorro:
Janek! proszę, przestań rysować wykresy

wiem jak wyglądają, ale nie wiem gdzie popełniam
błąd.. obliczenia pokazałem,
z mojego wykresu wynika, że f rośnie w (−
∞;−2) i (2;1>, a meleje w <1;
∞)
wiesz co jest grane?

19 wrz 16:31
zorro: post dodałem zanim zobaczyłem Twoją kolejną odpowiedź.. szczerze mówiąc pogubiłem się, więć
dowiem się od nauczyciela w poniedziałek co i jak, tak chyba będzie najprościej...
dziękuje za poświęcony czas

19 wrz 16:34



 Może i koń by wiedział, ale ja nadal nie wiem
Może i koń by wiedział, ale ja nadal nie wiem 


 wiem jak wyglądają, ale nie wiem gdzie popełniam
błąd.. obliczenia pokazałem,
z mojego wykresu wynika, że f rośnie w (−∞;−2) i (2;1>, a meleje w <1;∞)
wiesz co jest grane?
wiem jak wyglądają, ale nie wiem gdzie popełniam
błąd.. obliczenia pokazałem,
z mojego wykresu wynika, że f rośnie w (−∞;−2) i (2;1>, a meleje w <1;∞)
wiesz co jest grane? 
