Wyznacz przedział monotoniczności, wklęsłość, wypukłość , ekstrema funkcji
aga: f(x)=xlnx
18 wrz 18:18
aga: i punkty przegięcia
18 wrz 18:18
Janek191:
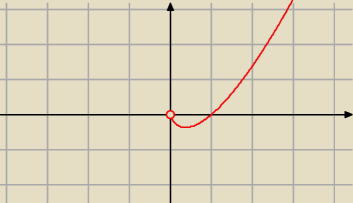
D = ℛ
+
f(x) = x*ln x
| | 1 | | 1 | |
f '(x) = ln x + x* |
| = ln x + 1 = 0 ⇔ ln x = − 1 ⇔ x = e−1 = |
| |
| | x | | e | |
więc
| | 1 | | 1 | |
f '' ( |
| } = e > 0 − funkcja w x = |
| ma minimum lokalne |
| | e | | e | |
f − jest wypukła
Dokończ
18 wrz 18:33
Janek191:
f jest wypukła w ( 0 ; +∞), bo f '' (x) > 0 w tym przedziale.
18 wrz 18:36
Janek191:
| | 1 | | 1 | | 1 | | 1 | |
ymin = f( |
| ) = |
| *ln ( |
| ) = − |
| |
| | e | | e | | e | | e | |
18 wrz 18:43
Janek191:
I gdzie ta Aga: ?
18 wrz 21:35