ekstrema i monotoniczność funkcji nie umiem obliczyć dalej
Łukasz: mam do rozwiązania takie oto zadanie:
Znajdź ekstrema i przedziały monotoniczności funkcji:
y=e
−2x2+2x
i nie mam pojęcia jak to ugryźć, pomóżcie

zacząłem od dziedziny Df:x∊R
y'=(e
−2x2)'+(2x)'=−4xe
−2x2+2
przyrównałem do zera
y'=0
−4xe
−2x2+2=0
i na tym się skończyło (co zrobiłem źle / co mam zrobić)?

17 wrz 21:10
:): jest ok, kontynuuj
17 wrz 21:15
Łukasz: tylko właśnie nie wiem jak

17 wrz 21:19
Nuti: Zbadaj pochodną
− kiedy ujemna (tam funkcja maleje)
− kiedy dodatnia (tam funkcja rośnie)
− kiedy równa 0 i zmienia znak (z plusa na minus − max, z minusa na plus − min). To Ci da
ekstrema lokalne.
Ekstrema globalne − zbadaj granicę f w plus i minus ∞ i zobacz, co tam się dzieje.
17 wrz 21:20
Łukasz: 4xe−2x2=2
xe−2x2=1/2
i co dalej?
17 wrz 21:22
Łukasz: to wszystko wiem, tylko nie mam pojęcia jak rozwiązać równanie po przyrównaniu do "0"
17 wrz 21:24
Nuti: A, teraz widzę, że to zero pochodnej nie jest takie oczywiste... Przepraszam, że nie
zrozumiałam Twojej trudności! Zastanowię się, też tak od razu nie widzę...
17 wrz 21:26
:): z tego co aptrze na wykres...to zdjae sie ze funkcja jest cały czas rosnaca i nie ma ekstremum,
teraz pasowaloby to ladnie uzasadnic

17 wrz 21:27
J:
Zadanie niebanalne .... moim zdaniem pochodna jest stale ujemna i funkcja stele malejąca
17 wrz 21:28
PW: Liczba 0 nie jest rozwiązaniem. Dla pozostałych x równoważne równanie ma postać
Obie funkcje umiemy narysować, więc może choć odpowiemy sobie ile jest rozwiązań i gdzie "mniej
więcej" leżą.
17 wrz 21:29
J:
rozpatrujemy równanie: 2x = ex2 ... graficznie , ex2 leży nad prostą : y = 2x ,
zatem: 2x − ex2 < 0
17 wrz 21:30
henrys: 
17 wrz 21:30
:): | | 1 | |
ja bym też sie pbawił funkcją g(x):=x*e−2x2− |
| i pokazał, że jest <0 zawsze |
| | 2 | |
17 wrz 21:31
Łukasz: nie da się tego rozwiązać w jakiś inny sposób?
17 wrz 21:32
J:
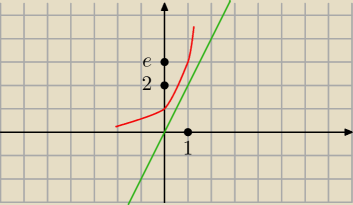
..myślę,że tak to wygląda
17 wrz 21:32
:): funkcja g, jest dość łatwa w "badaniu" wiec spokojnie mozesz to analitycznie pokazać
17 wrz 21:33
Łukasz: fajne miałem zadania na zaliczenie matmy? w sobotę poprawka a ja nie mam pojęcia jak to
rozwiązać
17 wrz 21:34
:): nie no..zadanie wydaje sie wieloetapowe, ale spokojnie dasz rade

Spokojnie

17 wrz 21:35
:): | | 1 | |
widać, że z g szybko sie robi − |
| i funkcja ma maksium w 1/2 (ujemne) |
| | 2 | |
17 wrz 21:40
:): szybko się robi =w granicy,gdy (x→+∞ lub x→−∞), ale dość szybko...
17 wrz 21:43
:): Jak ktoś to jeszcze czyta..

to f'(x)=−4*g(x) wiec f'(x)>0
17 wrz 21:47
Nuti: @Łukasz
Widzę, że jest dużo ochotników na Twoje interesujące zadanie

Na jakim to poziomie (która klasa)?
17 wrz 21:48
Nuti: @: ):
Czytamy z zapartym dechem!
17 wrz 21:49
:): : )))
17 wrz 21:50
Łukasz: studia politechnika

17 wrz 22:30
Łukasz: kierunek mechatronika, dzieki za pomoc jutro jeszcze nad tym posiedze moze cos wykombinuje

17 wrz 22:31
Nuti: @Łukasz
Powodzenia!
17 wrz 22:39
PW: Nierówność
ex2 > 2x
jest oczywista dla ujemnych x, może dla dodatnich wziąć kilka wyrazów rozwinięcia w szereg
ex2?
17 wrz 22:49
Nuti: @PW
O! To brzmi całkiem niegłupio! (Nie jestem zaskoczona, tylko się ucieszyłam.)
17 wrz 22:51
Janek191:
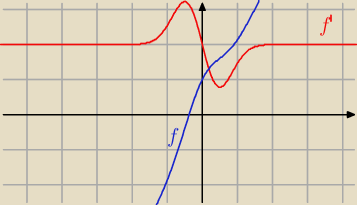
17 wrz 22:54
Nuti: Ale cudaki! (wykresy)
17 wrz 23:00
Łukasz: zastanawia mnie jeszcze jedno skąd wam się wzięło ex2?
w zadaniu jest e−2x2 i równa się 1/e2x2 więc jest to ukryte dzielenie
18 wrz 13:03
Nuti: −4xe
−2x2+2=0
2xe
−2x2=1
2x=e
2x2
(w trzecim wierszu e
2x2 w mianowniku − brzydko się narysowało...)
to samo przy nierównościach większe i mniejsze od zera. Można pomnożyć obie ich strony przez e
do odpowiedniej potęgi, bo e do czegokolwiek jest dodatnie, więc znak nierówności się nie
odwróci.
Jasne?
18 wrz 14:32
Łukasz: a teraz tak

18 wrz 15:01
PW: Tak, zgubiłem dwójkę (prawdę mówiąc powtórzyłem z 17.09. o 21:30), ale chyba problem nie polega
na tym? I jego rozwiązanie nie polega na użyciu maszyny do rysowania wykresów.
18 wrz 21:21
 zacząłem od dziedziny Df:x∊R
y'=(e−2x2)'+(2x)'=−4xe−2x2+2
przyrównałem do zera
y'=0
−4xe−2x2+2=0
i na tym się skończyło (co zrobiłem źle / co mam zrobić)?
zacząłem od dziedziny Df:x∊R
y'=(e−2x2)'+(2x)'=−4xe−2x2+2
przyrównałem do zera
y'=0
−4xe−2x2+2=0
i na tym się skończyło (co zrobiłem źle / co mam zrobić)? 



 ..myślę,że tak to wygląda
..myślę,że tak to wygląda
 Spokojnie
Spokojnie 
 to f'(x)=−4*g(x) wiec f'(x)>0
to f'(x)=−4*g(x) wiec f'(x)>0
 Na jakim to poziomie (która klasa)?
Na jakim to poziomie (która klasa)?



