rozwiąż równanie x-|x+2|=4 Dominik: rozwiąż równanie x−|x+2|=4 x≥−2 x−x−2=4 0=6 równanie sprzeczne lub x<−2 x+x+2=4 2x=2 x=1 nie należy do dziedziny czyli równanie nie ma rozwiązania?

J: a dlaczego x= 1 nie należy do dziedziny ?

:): moze nie tyle nie należy do dziedziny, co nie jest objęty warunkiem. Ale tak wygląda ok

Dominik: Znaczy sie nie spełna x<−2 a do dziedziny należy

J: bzdura: x ∊ R ⇔ Ix+2I = x − 4 ⇔ x+ 2 = x − 4 lub x + 2 = − x + 4 ⇔ 0 = −6 lub 2x = 2 ⇔ x= 1

Dominik: Dzięki za pomoc

:): Nie, miałeś racje Dominik

J: co znaczy: "wygląda ok" ? równanie ma rozwiązanie: x = 1

:): no nie ma

J: zaćmienie ... wycofuję swoje posty.

PW: Dobrze myśli, tylko słabo argumentuje. Dla x < − 2 mamy rozwiązać nierówność x − (− x −2) = 4, x∊(−∞, −2) 2x + 2 = 4, x∊(−∞, −2) x = 1, x∊(−∞, −2) Teraz widać, że równanie nie ma rozwiązania. Takie przepisywanie dziedziny może jest nudne, ale jest zalecane − żeby jej nie pomylić i w związku z tym poprawnie opowiedzieć, czy wyliczona liczba jest rozwiązaniem,

henrys: albo można by i tak: x−4=|x+2|≥0 x≥4 i mamy to samo

J: dokładnie tak ... przy moim sposobie rozwiązania musi być założenie: x − 4 ≥ 0

henrys: ale dziedziną tego równania jest x∊R

PW: Bywa, że mylone są "założenia" w sensie "dziedzina równania" z założeniami będącymi elementem myślenia (procesu rozwiązywania). Oczywiście dziedziną równania jest R. Najskuteczniejszym sposobem rozwiązania jest przekształcenie do postaci |x + 2| = x − 4 i spostrzeżenie: lewa strona równania jest liczbą nieujemną, takąż musi być prawa strona, wobec tego nie będziemy szukać rozwiązań tam, gdzie ich nie ma, to znaczy dla takich x, dla których x − 4 < 0. Ograniczamy się w dalszym ciągu do takich x, które spełniają nierówność (1) x − 4 ≥ 0. Zawężenie dziedziny poszukiwań niektórzy nazywają założeniem, ale mało kto pisze o tym tak wyraźnie. Rozwiązujemy więc równoważne równanie |x + 2| = x − 4, x∊[4,∞). Równoważne w tym sensie, że (jeśli w ogóle są), to rozwiązania obu równań należą do zbioru [4,∞) i są takie same.

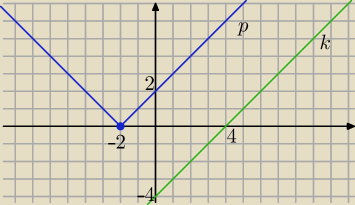
Eta: Metoda graficzna : |x+2|=x−4 f(x)=|x+2| i g(x)=x−4 ....proste k∥p wykresy nie mają punktów wspólnych Odp: takie równanie nie ma rozwiązań

:): Mam juz dość tego zadania ....

Eta: