symetria dixon: Hej. Mam problem z zadaniem ze sprawdzianu z symetrii. Mając dwa różne punkty A, B i prostą k równoległą do odcinka AB. skonstruuj punkt X należący do prostej k, tak aby obwód trójkąta AXB był najmniejszy.

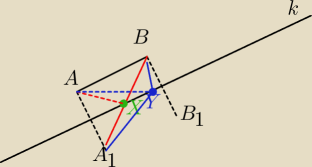
Nuti: Odbijasz A i B w symetrii osiowej względem k i łączysz np. A z obrazem B (albo odwrotnie, na to samo wyjdzie). X jest punktem przecięcia tego odcinka z k. Rzecz w tym, że przy takim wyborze X obwód trójkąta jest równy długości odcinka BA₁ (w tym przypadku jest to to samo co długość AB₁), a w każdym innym przypadku byłby równy długości łamanej (na granatowo i Y)

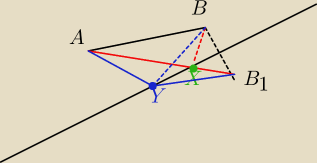
Nuti: Rozwiązanie działa zresztą równie dobrze (ta sama metoda), gdy AB nie jest równoległy do k! Zresztą głupio napisałam w poprzednim rozwiązaniu. ZAWSZE jest AB₁ = BA₁ (długości), ze względu na symetrię!