Proszę o pomoc :( majster: W trapez prostokątny ABCD, w którym AB|DC i AB⊥AD, wpisano okrąg o środku O. Udowodnij że kąt BOC jest prosty.

majster: Ma ktoś jakiś pomysł/podpowiedź jak to zrobić?

Nuti: To jest super łatwe, mogę zrobić rysunek za jakąś godzinę, bo teraz mam coś do załatwienia. Podpowiedź: narysuj, to będziesz widział! Pojawią się pewne trójkąty podobne i przystające.

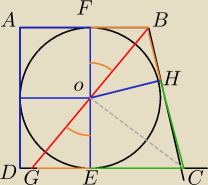
Nuti: Skoro w ten trapez można wpisać okrąg i trapez jest na dodatek prostokątny, to niebieskie odcinki zaznaczone na rysunku wszystkie mają długość r (promienia okręgu wpisanego). Również BF i BH mają równe długości, a także EC i CH (odcinki stycznych z tego samego punktu ). Przedłużamy odcinek BO do przecięcia G z odcinkiem DC. Trójkąty OBF i OEG są przystające (cecha BKB), czyli OB i OG są równej długości. Trójkąt GBC jest równoramienny (równe są ramiona BC i CG − to też ze względu na odcinki stycznych), a odcinek CO pada na środek trzeciego boku. Musi to więc być jego wysokość (i dwusieczna, i środkowa), czyli kąt BOC jest prosty, co należało pokazać.

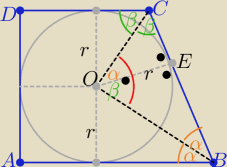
Eta: W każdym trapezie : 2α+2β=180^o ⇒ α+β=90^o odcinki OB i OC zawierają się w dwusiecznych kątów ABC i DCB wynika to z warunku wpisania okręgu w trapez zatem trójkąty AOE i COE są podobne z cechy (kkk) to |∡BOC|=α+β= 90^o c.n.w.

majster: Dziękuję