:) Krzyś :

	x2−x+1
Określ zbiór wartości funkcji f określonej wzorem: f(x)=
	x−1

Nuti: Policz granicę w plus i minus nieskończoności i prawo− i lewostronne granice w −1. Może już to Ci załatwi całe R Jeśli nie − poszukaj minimów i maksimów. Lokalnych, może globalnych...

Nuti: Powiedz, jeżeli sobie nie poradzisz, wtedy pomogę. Ale spróbuj.

5-latek: wpisz w wyszukiwarke Mila zbior wartości

Nuti:

Krzyś : Byłbym wdzięczny gdybyś mi pomogła.

Janek191: ZWf = ( −∞ ; − 1 > ∪ < 3; +∞ )

Janek191:

	x2 − x + 1
f(x) =		; x ≠ 1
	x − 1

więc

	( 2 x − 1)*( x −1) − ( x2 − x + 1)*1
f '(x) =		=
	( x −1)2

	2 x2 − 2 x − x + 1 − x2 + x − 1		x2 − 2x
=		=		=
	(x −1)2		(x −1)2

	x*(x −2)
=		= 0 ⇔ x = 0 lub x = 2
	(x −1)2

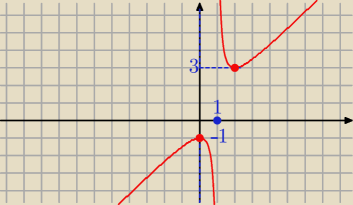
W x = 0 pochodna zmienia znak z + na minus − maksimum lokalne W x = 2 pochodna zmienia znak z − na plus − minimum lokalne W ( − ∞ ; 0 ) funkcja f rośnie , a w ( 0; 1) funkcja maleje W ( 1 ; 2) funkcja f maleje , a w ( 2 ; +∞) funkcja rośnie f( 0) = y_{max lok} = − 1 f(2) = y_{min lok} = 3 Wniosek : ZWf = ( − ∞ ; 1> ∪ < 3; +∞ ) =============================== Patrz też na wykres danej funkcji

Mila: Niech w będzie wartością funkcji f(x)⇔

x2−x+1
	=w
x−1

x²−x+1=w*(x−1) x²−x+1−wx+w=0 x²+x*(−1−w)+(w+1)=0 Równanie ma rozwiązanie dla Δ(w)≥0 Δ=w²−2w−3 w²−2w−3=0, Δ_w=16 w=−1 lub w=3 w²−2w−3≥0⇔ w≤−1 lub w≥3⇔ w∊(−∞,−1>∪<3,∞)=Zw_f