Informatyka , programowanie thola: dane są suma długości przekątnych rombu i długość jednego boku, jak wyliczyć pojedynczą przekątną? Potrzebuję żeby to był gotowy wzór. PROSZĘ O Pomoc

thola: Tylko teoretycznie, proszę

Nuti: W rombie wszystkie boki są równej długości. Masz jeden −− masz wszystkie. Zastanowię się nad wzorem. Ale pewnie ktoś mnie uprzedzi Co to znaczy teoretycznie? Sam gotowy wzór bez wyprowadzenia? Czy bez programu? (nie zamierzałam) Czy ma być z dowodem?

thola: Nie, to ma być suchy wzór, to znaczy bez liczb, bez wartości. Musze stworzyć schemat blokowy i tylko wpisać to co komputer miałby obliczyć czyli wzór na obliczenie każdej przekątnej z ich sumy i długości boków. Wiec mam sumę przekątnych−s i długość boku−a, czego wynikiem będą e i f. Byłabym wdzięczna baaardzo za pomoc.

pigor: ... niech 2d+2e= s − dana suma przekątnych i a −dana długość boku, to masz układ równań 2d+2e=s i d²+e²=a² , gdzie d,e=? połowy przekątnych − niewiadome ..

PW: Gdyby matematyka polegała na pamiętaniu "gotowych wzorów", to większość z nas miałaby schizofrenię. Niepotrzebnie mówisz "długość jednego boku" − w rombie wszystkie boki mają jednakowe długości, więc wystarczy "długość boku". Wiadomo, że w rombie przekątne są wzajemnie prostopadłe i połowią się.

	d1		d2
Mamy więc trójkąt prostokątny o przyprostokątnych		i		(to są połowy
	2		2

przekątnych) i przeciwprostokątnej a (to jest długość boku rombu). Trzeba więc rozwiazać układ równań:

	⎧	(0,5d1))2 + (0,5d2)2 = a2
	⎨		,
	⎩	d1+d2 = s

gdzie s jest znaną sumą długości przekątnych. Jeżeli chcesz wyliczyć tylko jedną przekątną, np. d₂, to z drugiego równania wyliczasz d₁ = s − d₂ i podstawiasz do pierwszego równania − będzie równanie kwadratowe zmiennej d₂ − komputer ma szukać tylko rozwiązania dodatniego.

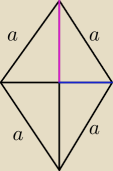
Nuti: Przekątne w rombie dzielą się na połowy i na dodatek pod kątem prostym. Oznacz długość boku (daną) przez a, a sumę długości przekątnych przez S. Jeżeli oznaczyć długości przekątnych przez d₁ i d₂, to z twierdzenia Pitagorasa mamy:

	1		1
(		d1)2+(		d2)2=a2
	2		2

d₁+d₂=S, czyli

1		1
	d12+		(S−d1)2=a2
4		4

i masz równanie kwadratowe na d₁, ze znanymi (danymi) współczynnikami (jakieś liczby, a i S). Porządkujesz je i rozwiązujesz i otrzymasz zapewne dwa pierwiastki dodatnie. Jeden z nich to będzie d₁, a drugi d₂. Poradzisz sobie, czy mam to zrobić?

Nuti: równanie do rozwiązania (komputer umie?) to

	1
x2−Sx+		S2−2a2=0.
	2

thola: Nie rozumiem nic. Mógłby ktoś zrobić to łopatologicznie dla mnie na liczbach? Może wtedy zrozumiem.

Nuti:

	1		1
Nawet rysunek zrobiłam. To różowe to		d1, a granatowe		d2. No i twierdzenie
	2		2

Pitagorasa. Na pewno znasz!

thola: Znam, znam, ale co mi to da ze go oblicze?

Nuti: No to, że masz teraz równanie kwadratowe, z którego możny wyliczyć długości przekątnych.

	1
x2−Sx+		S2−2a2=0.
	2

a i S są dane, masz obliczyć x. Delta, pierwiastki i już.

Nuti: Chyba że to nie jest dobra postać rozwiązania dla komputera. Ale algorytm to sobie sam musisz napisać. Może będzie prościej korzystając z rozwiązań innych kolegów (Eta, PW, pigor). Wszyscy w każdym razie korzystamy z Pitagorasa, ale może któryś zapis jest szczególnie odpowiedni do napisania algorytmu. Nie znam się na tym.

Nuti: Jeżeli na przykład a to 5, a suma przekątnych (S) to 14, Twoje równanie wygląda następująco: x²−14x+48=0 Δ=196−192=4

	14+2
d1=		=8
	2

	14−2
d2=		=6
	2

czyli przekątne mają długości 6 i 8.

PW: Wzór

	S2
x2 − Sx +		− 2a2 = 0
	2

świetnie nadaje się do obliczeń:

	S		S2		S2
(x −		)2 −		+		− 2a2 = 0
	2		4		2

	S		S2
(*) (x −		)2 = 2a2 −
	2		4

(po prostu najpierw kochaneczek obliczy prawą stronę, potem pierwiastek z niej i na końcu doda 0,5S). Schemat blokowy już jest: stosujemy wzór (*), 1. Liczymy a*a 2. Podwajamy wynik z p. 1. 3. Liczymy S*S 4. Liczymy 0,25 wyniku z p. 3 5. Od wyniku nz p. 2. odejmujemy wynik z p. 4. 6. Liczymy pierwiastek liczby otrzymanej w p. 5. 7. Do wyniku z p. 6. dodajemy 0,5S − to jest szukana przekątna oznaczona symbolem d₁ przez Nuti. W ten sposób obliczymy dłuższą przekątną − tę która jest większa od połowy sumy S (bo przyjmujemy, że pierwiastek z (x − 0,5S)² jest dodatni. Drugą przekątną liczymy po prostu odejmując pierwszą od S: d₂ = S − d₁ Byłby to 8. punkt schematu blokowego (proszę wybaczyć niefachowość).

Nuti: No to super! Wygląda na to, że jakoś tam pomogliśmy. Co Thola sądzi na ten temat? Wszystko jasne?

Nuti: Podoba mi się ten schemat blokowy!

PW: Pytająca straciła zainteresowanie, ale dla spokoju sumienia sprostuję jeden niuans. Gdyby liczba wyznaczona w p. 5. okazała się zerem, to komputer może odpocząć − szukana przekątna ma długość równą połowie S, czyli przekątne są równych długości − wypisuje odpowiedni komunikat. Przydałoby się również zabezpieczenie przed nieprawidłowymi danymi − jeżeli liczba wyznaczona w p.5. okaże się ujemna, to przerywamy obliczenia i wypisujemy komunikat "Nieprawidłowe dane − nie ma takiego rombu". Komunikat o nieprawidłowych danych powinien się pojawić już w p. 1 − gdyby wczytana liczba a okazała się niedodatnia lub w p. 3. − gdyby S okazała się niedodatnia. I tak dalej, program można udoskonalać do świtu.

Nuti: No i połowa S musi być większa od a (nierówność trójkąta)... O tym nawet nie wspominałam, bo zakładałam, że skoro „dany jest romb", to wszystko musi w nim być Ok Ale masz rację, @PW, chyba nie mamy do kogo gadać...

hellos: Doda ktoś kod w C++?

darek: Totalne oro w pythonie nie wiem jak zrobic pomoze ktos? import math a=float(input("Wprowadz dlugosc boku:")) s=float(input("Podaj sume przekatnych rombu:")) x=1 def kekw(): lewa=(x−s/2)**2 print(lewa) def kaki(): prawa=2*(a**2)−(s**2)/4 print(prawa) jedynka=a**2 dwojka=2*jedynka trojka=s**s czworka=0.25*trojka piatka=dwojka−czworka szostka=(math.sqrt(piatka)) siodemka=szostka+(0.5*s) print(siodemka) osemka=s−siodemka print(osemka)

Filip: ale co chcesz zrobić?

darek: kocham vl

k4p3k: Problem już rozwiązany u kolegi na pv