Rozwiąż nierówności Przemek: Rozwiąż nierówności:

	|2x−5|
a)		≤ 2
	|x+1|

	x2+9x+8
b)		≥ 1
	x2−9x+8

	x2−7|x|+10
c)		< 0
	x2−6x+9

Proszę o wytłumaczenie.

PW: a) Dziedzina: x ≠ −1

	|a|		a
Można skorzystać z faktu, że		= |		|, czyli rozwiązać nierówność
	|b|		b

	2x − 5
|		| ≤ 2, x∊R\{−1}
	x + 1

Taka nierówność jest równoważna podwójnej nierówności

	2x − 5
−2 ≤		≤ 2, x∊R\{−1}
	x + 1

to znaczy układowi dwóch nierówności:

	2x − 5		2x − 5
− 2 ≤		∧		≤ 2, x∊R\{−1}.
	x + 1		x + 1

Dalej powinno być bez kłopotów, doprowadzić do postaci z zerem po jednej stronie. Wystarczy tłumaczenia?

Przemek: Dzięki

Przemek: Po obliczeniu mam tak: (4x−3)(x+1) ≥ 0 ⋀ −3x−3 ≤ 0

PW: Drugie sprawdź jeszcze raz.

Przemek:

2x−5		2x−2
	−		≤ 0
x+1		x+1

−3
	≤ 0
x+1

−3(x+1) ≤ 0 −3x−3 ≤ 0 x=−1 ?

5-latek: −3x−3≤0 −3x≤3 x≥−1

Przemek: Ok. Faktycznie jak dzieli się przez ujemną liczbę to zmienia się znak.

pigor: ..., np. tak :

	x2−7|x|+10
c)		< 0 ⇒ (x2−7|x|+10) (x2−6x+9) < 0 ⇔
	x2−6x+9

⇔ (|x|−5) (|x|−2) (x−3)²< 0 i x∊R\{3} ⇔ ⇔ (x<0 i (−x−5)(−x−2)(x−3)²<0) v (x ≥0 i x≠3 i (x−5)(x−2)(x−3)²<0) ⇔ ⇔ (x<0 i (x+5)(x+2)(x−3)²<0) v (2< x < 3 v 3< x < 5) ⇔ ⇔ −5< x< −2 v (2< x< 3 v 3< x< 5) ⇔ x∊(−5;−2) U (2;3) U (3;5)....

Aga1.: a)np tak

I2x−5I
	≤2 /*Ix+1I , bo dla x≠−1 Ix+1I>0
Ix+1I

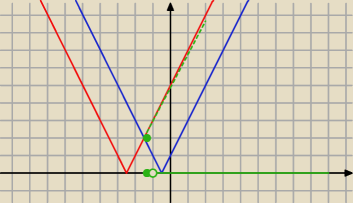
I2x+5I≥2Ix+1I I2x+5I≥I2x+2I i jeśli umiesz rysować wykresy to dalej graficznie f(x)=I2x+5I, g(x)=I2x+2I