Granica Ewelonka: Wyznacz granice jednostronne funkcji y=−x² −2 +1 / (x−3)²

Ewelonka: X=3

Janek191:

	− x2 − 2 x − 1
y = f(x) =		?
	( x −3)2

x → 3 ?

Ewelonka: No tak , tylko mi się źle napisało ... sorka

Ewelonka: Tylko tam +1

Janek191:

	− x2 − 2 x + 1		−9 − 6 + 1
lim		=		= − ∞
	( x −3)2		0+

x→ 3⁻

	− x2 − 2 x + 1		− 9 − 6 + 1
lim		=		= − ∞
	(x −3)2		0+

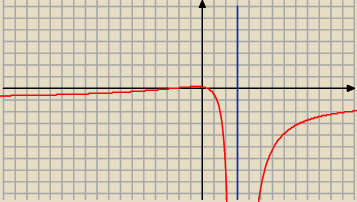
x→ 3⁺ Patrz też na wykres funkcji f :

Ewelonka: Czyli u góry możemy sobie podstawić ta 3 , tak ? A wykres to bierze się z tego wyrażenia u dołu ?

Janek191: ( x − 3)² jest zawsze dodatnie i dąży do 0 , gdy x → 3 ( z lewej czy z prawej strony ), natomiast licznik dąży do liczby ( − 14) Dlatego otrzymujemy granicę niewłaściwą równą −∞

Ewelonka: A na tej zasadzie 😊 baaardzo Ci dziękuję za pomoc 😉 A mam jeszcze pytanko tak dla upewnienia ten przykład : Nie znam skrótów do tego żeby ładnie to napisać , ale dobra lim (modul) x−3 (moduł) / x−3 przy x→3⁻

Ewelonka: Tu moduł zawsze będzie dodatni, a mianownik ujemny, ale rozwiązanie to −1 , czyli mam dzielenie +∞ : − ∞ = −1 ?

Ewelonka: Tu moduł zawsze będzie dodatni, a mianownik ujemny, ale rozwiązanie to −1 , czyli mam dzielenie +∞ : − ∞ = −1 ?

Janek191:

	I x − 3 I
lim		?
	x − 3

x→ 3⁻

Ewelonka: Chyba mi się pomieszało to wszystko 😕

Ewelonka: Tak

Janek191: Dla x < 3 jest I x − 3 I = −( x − 3) = 3 − x więc

	I x − 3 I
lim		= − 1 z reguły de l ' Hospitala
	x − 3

x→ 3⁻

Ewelonka: A no ja nie miałam takiej reguły ... czyli po prostu opuszczamy moduł z przeciwnym znakiem bo pod modułem jest ujemna ?

Janek191:

	0
Mamy symbol nieoznaczony		i dlatego stosujemy regułę de l ' Hospitala
	0

	− 1
... = H		= − 1
	1

Pochodna licznika jest równa (−1) , a pochodna mianownika jest równa 1.

Ewelonka: A ok 😉 jeszcze raz wieeelkie dzięki 😊 musze sobie to teraz po swojemu przetłumaczyć...

Janek191: Poczytaj po lewej stronie ( kolor niebieski ): Granica ciągu i funkcji. Wyrażenia nieoznaczone.

Ewelonka: Dzięki 😉 na pewno skorzystam ☺