Zbadać monotoniczność i znaleźć ekstrema funkcji: Natalia: Zbadać monotoniczność i znaleźć ekstrema funkcji:

	4
f(x)=x+
	x

Proszę o wytłumaczenie krok po kroku jak to zrobić. O ile dobrze kojarzę, liczy się to z pochodnych, ale nie mam pojęcia od czego zacząć.

Braun: 1. Policz pochodną.

Braun: Jak zrobisz to będziemy działać dalej ! Tylko przed pochodną, dziedzina (obowiązkowo)

Janek191:

	4
f(x) = x +
	x

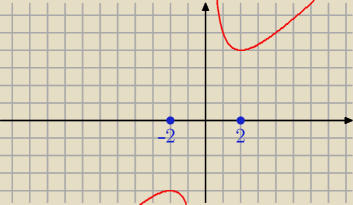
x ≠ 0

	4
f ' (x) = 1 −		= 0 ⇔ x = − 2 lub x = 2
	x2

	8
f ''(x) = − 4*(−2)*x−3 =
	x3

Mamy: f ''( − 2) = − 1 < 0 − w punkcie x = − 2 funkcja f ma maksimum lokalne f ''( 2) = 1 > 0 − w punkcie x = 2 funkcja ma minimum lokalne Dla x ∊ ( − 2 ; 2) \ { 0 } jest f ' (x) < 0 − zatem f maleje w przedziałach : ( − 2 ; 0) , ( 0; 2) Dla x < −2 lub x > 2 jest f '(x) > 0 − funkcja f rośnie w : ( −∞ ; −2) , ( 2 ; +∞ )

Natalia: Dziedzina: "x" różne od "0". Pochodna:

	4
1 −
	x2

Natalia: janek − dzięki ślicznie

Braun: Janek daj pomyśleć ludziom...

Janek191: Chciała " krok po kroku "