prosze o sprawdzenie cal45: Wyznacz przedziały monotoniczności funkcji f. a) f(x) = x³ − 3x − 5 rośnie w (−∞;−1) i (1;∞) maleje w (−1;1) b) f(x) = x⁵ − 20x + 1 rośnie w (−∞; −√2) i (√2;∞) maleje w (−√2;√2) c) f(x) = 6x⁵ + 5x³ + 6 rośnie w (0;∞) maleje w (−∞;0)

J: i co ?

J: aaaa...chcesz sparawdzenia... a) OK

cal45: Zwracam się z prośbą o sprawdzenie, ponieważ w podręczniku nie mam odpowiedzi

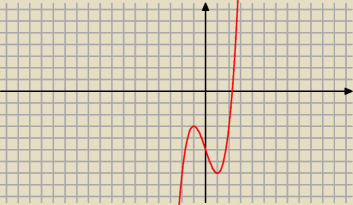
Janek191: a) Powinno być: f rośnie w: ( −∞ , − 1) , ( 1 ; + ∞ ) Bez " i"

J: może być "i" ... bo rośnie w obydwu przedziałach jednocześnie

cal45: dzięki za a). Pozostałe też dobrze?

J: b) OK.

J: c) niestety...źle

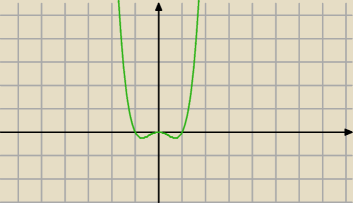
J: tutaj masz wykres pochodnej do przykładu c)

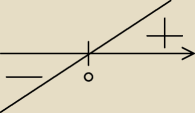
cal45: c) liczyłem tak: f(x) = 6x⁵ + 5x³ + 6 f'(x) = 30x⁴ + 15x² 30x⁴ + 15x² = 15x²(2x² + 1) = 0 z 15x²=0 x to 0, a z 2x²+1=0 nie ma nic narysowałem wykres i stąd taki wynik − co tutaj zrobiłem źle?

J: sorry..to ja się pomyliłem ...widziałem znak minius przed 5x³ ... jest dobrze

cal45: to fajnie, dzieki mam jeszcze trochę zadań/pytań z rachunku różniczkowego − powinienem stworzyć nowy temat do każdego czy w tym mogę pytać?

J: lepiej zakładaj nowy temat do każdego zadania

cal45: umieszczam tutaj, bo dalej liczę to samo zadanie − kolejne podpunkty d) f(x) = (x+3)²(x−1)

	1
f'(x) = 3x2 + 10x + 3 = 3(x+3)(x+		) (sprawdziłem wolframem)
	3

	1
rośnie w (−∞;−3> i <−		;∞)
	3

	1
maleje w <−3;−		>
	3

dobrze? e)

	2x−1
f(x) =		, Df=R\{2}
	x−2

	−3
f'(x) =		(sprawdziłem wolframem), Df'=R\{2}
	(x−2)2

pytanie co dalej, normalnie licznik przyrównuję do zera, ale tutaj wychodzi −3=0... f)

	x2−7
f(x)=		, Df=R\{4}
	x−4

	(x−7)(x−1)
f'(x)=		(sprawdziłem wolframem), Df'=R\{4}
	(x−4)2

rośnie w (−∞;1> i <7;∞) maleje w <1;7> tak?

cal45: zobaczycie na te 3 przykłady?

J: ad e) ... pochodna ma stały znak ( ujemny), a więc funkcja maleje w całej dziedzinie

J: d) i f) ..dobrze

cal45: dzięki bardzo