Trójkąt w geometrii analitycznej. Kavaler: Najdłuższy bok trójkąta ma długość 5, a najkrótszy ma długość 2. Jakie jest największe pole trójkąta spełniającego te warunki?

pigor: ..., czy może P_max= 5 ...

Kavaler: Tak, ale jak to obliczyć

PW: Możesz spróbować wzoru Herona, w końcu dwa boki są, więc otrzymasz funkcję jednej zmiennej Trzeci bok x spełnia nierówność 3 < x ≤ 5 (suma dwóch boków musi być większa od 5, czyli 2+x > 5). Jeżeli zdołasz rozwiązać "zadanie optymalizacyjne", to odpowiedź gotowa. Dlaczego dałeś hasło "trójkąt w geometrii analitycznej"?

Janek191: P = 0,5*5*2 *sin α = 5 dla α = 90^o sin α ≤ 1 , bo α > 0^o i α < 180^o

PW: Trochę żartuję. pomyśl o tym co napisał pigor. Pole trójkąta to połowa iloczynu podstawy i wysokości

pigor: ..., o już jest, no właśnie, ja tak jak Janek, jeśli α − miara kąta Δ między danymi bokami, to z własności sinusa takiego kąta, jego pole : P= ¹₂*2*5sinα= 5sinα ≤ 5*1= 5= P_max dla α=90^o, no i tyle. ... −−−−−−−−−−−−−−−−−−− p.s. z wzoru Herona też , ale trochę roboty, bo np. tak :... niech 2<x<5, to P²(x)= p(p−2)(p−x)(p−5)= ...=− ¹₁₆(x²−49)(x²−9) − funkcja kwadratowa ze względu na x², a więc dla x²=¹₂(49+9)= ¹₂*58=29 P²(29}= − ¹₁₆(29−49)(29−9)= ¹₁₆*20*20=25= P²_max ⇒ P_max= 5

PW: Ja jeszcze prościej (myślałem, że tak liczyłeś):

	1
P =		·5·h
	2

Wysokość trójkąta opuszczona na bok b nie przekracza długości krótszego boku różnego od b (tu przydałby się rysunek), pole jest więc największe, gdy wysokość jest równa długości boku, czyli gdy trójkąt jest prostokątny o przyprostokątnej h = 2.

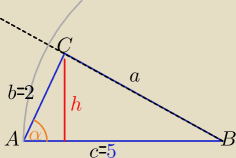
Mila: h<2