Obliczyć pochodną całej funkcji ola: Obliczyć pochodną całej funkcji. Dla jakich a,b,c pochodna jest taka sama . . 4x. x<0 f(x) = ax²+bx+c. 0<x<1 . 3−2x. x>1

PW: Pochodna zawsze "jest taka sama". Co masz na myśli?

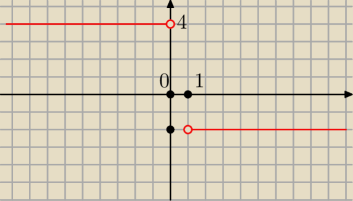
Nuti: Czy Twoja funkcja nie jest zdefiniowana w 0 i 1? Czy nie ma gdzieś nieostrej nierówności? Pochodna dla ujemnych jest stała, f'(x)=4 dla x<0 Dla x>1 pochodna też jest stała, f'(x)=−2 dla x>1. Dla 0<x<1 mamy f'(x)=2ax+b. Sprawdź, na jakie pytanie masz odpowiedzieć i spróbuj to zrobić na podstawie wyglądu (wzoru) pochodnej.

Nuti: Widzisz z wzoru f'(x)=2ax+b, że wartość c nie ma żadnego wpływu na pochodną. Gdy odnajdziesz właściwe pytanie, będziesz musiała wyliczyć odpowiednie a i b.