x
Psychopata: | | 3 | |
Wyznacz równania stycznych do wykresu funkcji f(x)= |
| i równoległych do prostej |
| | x | |
| | 1 | |
y=− |
| x. Podaj współrzędne punktów styczności tych prostych. |
| | 3 | |
Nie umiem tego zrobić...
Znam wzór na styczną y−f(x
0)=f'(x
0)*(x−x
0) gdzie
f(x
0) to wartość funkcji w punkcie styczności
x
0 to pierwsza współrzędna punktu styczności
f'(x
0) to wartość pochodnej funkcji dla punktu x
0
| | 1 | |
Styczne ponieważ będą równoległe to będą miały równanie y=− |
| x+b czyli punkt styczności |
| | 3 | |
| | 1 | |
będzie miał współrzędne (x0, − |
| x0+b). Aczkolwiek teraz jak podsatwiam do wzoru |
| | 3 | |
wychodzi bzdura (0 po prawej stronie równania)
14 wrz 20:38
14 wrz 20:40
Psychopata: Jak do tego doszedłeś

Ja tu nic nie rozumiem ...
14 wrz 20:41
J:
| | 1 | |
f'(x0) , to tangens nachylenia stycznej do osi OX ,czyli .... f'(x0)= − |
| |
| | 3 | |
14 wrz 20:43
Psychopata: y−f(x0)=f'(x0)*(x−x0)
Faktycznie, i co dalej

14 wrz 20:44
J:
| | 3 | | 1 | |
źle ... − |
| = − |
| ... i wyznacz punkty styczności |
| | (x0)2 | | 3 | |
14 wrz 20:47
Psychopata: o co ci chodzi

przecież jest wzór y−f(x
0)=f'(x
0)*(x−x
0)
| | −1 | |
pod f'(x0) podstawiłem już to |
| ale nie wiem co dalej i skąd się bierze twoje równanie |
| | 3 | |
ja chcę to zrozumieć a nie uczyć się na pamięć
14 wrz 20:48
J:
| | 1 | | 3 | | 1 | |
masz: f'(x0) = − |
| , czyli: − |
| = − |
| ⇔ |
| | 3 | | (x0)2 | | 3 | |
x
0 = 3 lub x
0 = − 3 ( dwa punkty styczności) , teraz liczysz f(x
0) i wsystko podstawiasz
do równania stycznej ... koniec ( dwie styczne)
14 wrz 20:52
Psychopata: | | 3 | | −1 | |
Nie rozumiem skąd się bierze − |
| = |
| |
| | (x0)2 | | 3 | |
Znam wzór y−f(x
0)=f'(x
0)*(x−x
0)
14 wrz 20:53
Nuti: pochodna w punkcie x0 to współczynnik kątowy stycznej w punkcie (x0,f(x0)).
14 wrz 20:56
J:
| | 3 | | 3 | | 1 | |
oprzytomniej .... f'(x) = − |
| , czyli: f'(x0) = − |
| = − |
| , |
| | x2 | | (x0)2) | | 3 | |
| | 1 | |
bo styczna ma być równoległa do prostej: y = − |
| x , czyli musi mieć ten sam współczynnik |
| | 3 | |
14 wrz 20:56
Mila:
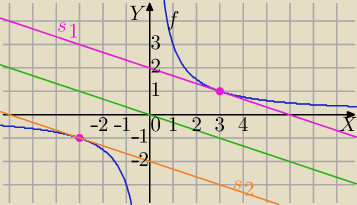
k:
Styczna :
y−f(x
0)=f'(x
0)*(x−x
0)
Nie znasz x
0, więc trzeba obliczyć.
Styczna jest prostą , jej współczynnik kierunkowy jest równy f'(x
0)
x
0=3 lub x
0=−3
(3,1),(−3,−1) punkty styczności
Styczne :
| | 1 | | 1 | |
s1: y=− |
| (x−3)+1⇔y=− |
| x+2 |
| | 3 | | 3 | |
lub
| | 1 | | 1 | |
s2: y=− |
| (x+3)−1⇔y=− |
| x−2 |
| | 3 | | 3 | |
14 wrz 21:03
J:
Może tak:
| | 1 | | 1 | |
dana prosta : y = − |
| x ....więc: tgα = − |
| |
| | 3 | | 3 | |
| | 1 | |
f'(x0) = tgα = − |
| , bo styczna i zadana prosta są równoległe ...jarzysz ? |
| | 3 | |
14 wrz 21:04
Psychopata: Aha....... a ja chciałem na siłe użyć wzoru z podręcznika. Nie wiem po kiego grzyba dali ten
je...ny wzór albo nie wszystko idzie nim zrobić. Ok mam x
0=3 lub x
0=−3
Czyli te punkty to (3,1) i (−3,−1)

14 wrz 21:04
Psychopata: Mila 
dziękuje

14 wrz 21:06
J:
tak ... teraz podstawiasz do rownania stycznej:
| | 1 | |
y − 1 = − |
| (x − 3) ... jedna styczna |
| | 3 | |
| | 1 | |
y + 1= − |
| (x + 3) ... druga styczna |
| | 3 | |
14 wrz 21:07
Psychopata: nie wiedziałem że współczynnik kierunkowy stycznej to f'(x
0)

| | f(x0)+h)−f(x0) | |
nie miałem tego w pazdze bo napisali tylko jeśli h→0 to tg β→tg α czyli |
| |
| | h | |
→ f'(x
0) tego też nie rozumiem ale mniejsza o to
14 wrz 21:13
Mila:
Przecież masz równanie stycznej w postaci kierunkowej i widać , że to równanie prostej
postaci:
y=ax+b.
Wsp. przy x to współczynnik kierunkowy prostej.
14 wrz 21:26
Mila:
Ad. 21:13
To jest obliczanie pochodnej w punkcie z definicji, musisz się tego nauczyć, jest na maturze,
styczne też są.
Spróbuj rozwiązać z książki (zbioru) przykład, jeśli nie wyjdzie, to wpisz tutaj.
14 wrz 22:42
 Ja tu nic nie rozumiem ...
Ja tu nic nie rozumiem ...

 przecież jest wzór y−f(x0)=f'(x0)*(x−x0)
przecież jest wzór y−f(x0)=f'(x0)*(x−x0)
 k:
k:

 dziękuje
dziękuje 
