Granica Qazz: Granice: lim_x−>0 (1−x)² lim_x−>0 (x)^x

:): obie 1

J: druga ,nie ... symbol nieoznaczony

:): jak najbardziej 1

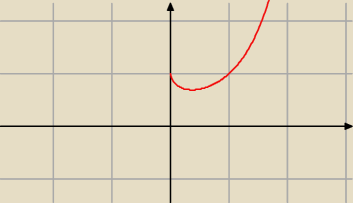
Janek191: f(x) = x^x

:): z drugiej strony...jest to bardziej skomplikowane bo jest tam funkcja zespolona..ale jednak też jest 1

Qazz: no właśnie jak sobie dać radę z tym nieoznaczonym?

:): ciągłość + 0⁰=1 KONIEC

J: 2) f(x) = e^x*lnx i lime^xln = 1 , bo gdy x → 0, to : xlnx → 0

J: 0⁰ ..to symbol nieoznaczony

:): tak jak pisałem...to jest z prawej...z lewej formalnie jest jeszcze urojona częśc itd... ale no będzie 1

Qazz: Bo właściwe polecenie to zadać ciągłość tej funkcji. Czyli zbadać granice w pkt 0, bo tam jest zmiana (a powinno się jeszcze przy lim podać 0+ lub 0− ?). I nie wiem jak właściwe policzyć lim dla x^x

:): J: tak, ogólnie 0⁰ to symbol nieznacozny ale nie mówie tu o granicach tylko o zwykłym 0⁰ (liczba do liczby), żadnnych granic.. takie coś =1

Qazz: aaa... dzięki, pisałem zanim pojawiły się odpowiedzi. i dla x^x, ponieważ jest dla funkcji x>0, to będzie 0+, a dla (x−1)², x<=0 0− ?

:): dla tej pierwsej funkcji jest to oczywiste,podstaw (bo mozesz) i tyle..

J: nie masz racji , 0⁰ nie równa sie 1

:): nie chce sie tu powoływać na swoje wykształcenie.....

:): policz sobie na kalkulatorze

J: no.... w kombinatoryce

:): formalnie... to przyjmuje, się że (0+)⁰⁺, tak naprawde jest to kwestia umowy, ale przemawia lwasnie za tym ciąglosc prawostronna funkcji x^x